
 ,動點P滿足
,動點P滿足 (O為坐標原點),點P的軌跡記為曲線C.
(O為坐標原點),點P的軌跡記為曲線C. 交于M、N兩點,求證:
交于M、N兩點,求證: 為定值.
為定值. ,知P是線段AB的中點,由此能得到點P的軌跡C的方程.
,知P是線段AB的中點,由此能得到點P的軌跡C的方程. ,知P為線段AB的中點,由M、N分別在直線y=x和y=-x上,知∠AOB=90°.由此能得到點P的軌跡C的方程.
,知P為線段AB的中點,由M、N分別在直線y=x和y=-x上,知∠AOB=90°.由此能得到點P的軌跡C的方程. =
= ,
, .聯立
.聯立 ,故
,故 .由此能夠證明
.由此能夠證明 •
• 為定值0.
為定值0. ,∴P是線段AB的中點,∴
,∴P是線段AB的中點,∴ (2分)
(2分) ,∴
,∴ ,∴
,∴ .
. .(5分)
.(5分) ,∴P為線段AB的中點、(2分)
,∴P為線段AB的中點、(2分) ,∴
,∴ ,∴點P在以原點為圓心,
,∴點P在以原點為圓心, 為半徑的圓上、
為半徑的圓上、 .(5分)
.(5分) =
= ,∴
,∴ .
. ,∴
,∴ .
. ,
, .(8分)
.(8分) •
• =x1x2+y1y2=
=x1x2+y1y2= .
. ,∴
,∴ •
• =0.(10分)
=0.(10分) ,代入橢圓方程得
,代入橢圓方程得 ,
, ),N(
),N( ,-
,- )或M(-
)或M(- ,
, ),N(-
),N(- ,-
,- ),
), •
• =
= -
- =0.
=0. •
• 為定值0.(12分)
為定值0.(12分)

 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案科目:高中數學 來源: 題型:
4
| ||
| 5 |
| OP |
| OA |
| OB |
| x2 |
| 4 |
| OM |
| ON |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
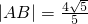 ,動點P滿足
,動點P滿足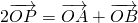 (O為坐標原點),點P的軌跡記為曲線C.
(O為坐標原點),點P的軌跡記為曲線C. 交于M、N兩點,求證:
交于M、N兩點,求證: 為定值.
為定值.查看答案和解析>>
科目:高中數學 來源:山西省模擬題 題型:解答題
 ,動點P滿足
,動點P滿足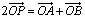 (O為坐標原點),點P的軌跡記為曲線C。
(O為坐標原點),點P的軌跡記為曲線C。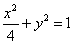 交于M、N兩點,求證:
交于M、N兩點,求證: 為定值。
為定值。查看答案和解析>>
科目:高中數學 來源:2011年河南省許昌市許昌縣一高高考數學模擬試卷4(文科)(解析版) 題型:解答題
 ,動點P滿足
,動點P滿足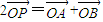 (O為坐標原點),點P的軌跡記為曲線C.
(O為坐標原點),點P的軌跡記為曲線C. 交于M、N兩點,求證:
交于M、N兩點,求證: 為定值.
為定值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com