
【題目】已知![]() 的三個頂點
的三個頂點![]() 均在拋物線
均在拋物線![]() 上,給出下列命題:
上,給出下列命題:
①若直線![]() 過點
過點![]() ,則存在
,則存在![]() 使拋物線
使拋物線![]() 的焦點恰為
的焦點恰為![]() 的重心;
的重心;
②若直線![]() 過點
過點![]() ,則存在點
,則存在點![]() 使
使![]() 為直角三角形;
為直角三角形;
③存在![]() ,使拋物線
,使拋物線![]() 的焦點恰為
的焦點恰為![]() 的外心;
的外心;
④若邊![]() 的中線
的中線![]() 軸,
軸,![]() ,則
,則![]() 的面積為
的面積為![]() .
.
其中正確的序號為______________.
【答案】①②.
【解析】
對于①設出直線![]() 方程,與拋物線聯立,利用韋達定理,求出
方程,與拋物線聯立,利用韋達定理,求出![]() 坐標和,再利用重心坐標公式,求出
坐標和,再利用重心坐標公式,求出![]() 點坐標,代入拋物線方程,即可得出結論;
點坐標,代入拋物線方程,即可得出結論;
對于②當直線![]() 過點
過點![]() ,可證
,可證![]() ,即可得出結論為正確;
,即可得出結論為正確;
對于③判斷以焦點為圓心的圓與拋物線是否有三個交點;
對于④設![]() 方程與拋物線聯立,利用韋達定理,求出
方程與拋物線聯立,利用韋達定理,求出![]() 中點坐標,然后轉化為
中點坐標,然后轉化為![]() 點坐標,將
點坐標,將![]() 點坐標代入拋物線方程,求出
點坐標代入拋物線方程,求出![]() 的面積,即可判斷結論是否正確.
的面積,即可判斷結論是否正確.
設![]() 三點坐標分別為
三點坐標分別為![]() ,
,
①直線![]() 過點
過點![]() ,設
,設![]() 方程為
方程為![]() ,
,
聯立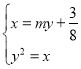 ,消去
,消去![]() ,得
,得![]() ,
,
![]() ,
,
拋物線![]() 的焦點恰為
的焦點恰為![]() 的重心,
的重心,
![]() ,
,
將![]() 點坐標代入拋物線方程
點坐標代入拋物線方程![]() ,
,
當![]() 時,
時,![]() ,①正確;
,①正確;
②直線![]() 過點
過點![]() ,設
,設![]() 方程為
方程為![]() ,
,
聯立![]() 消去
消去![]() 得,
得,![]() ,
,
![]() ,
,
![]() ,而點
,而點![]() 在拋物線上,故②正確;
在拋物線上,故②正確;
③設以拋物線焦點![]() 為圓心的圓半徑為
為圓心的圓半徑為![]() ,
,
其方程為![]() ,與拋物線方程聯立得
,與拋物線方程聯立得
![]() ,
,
方程至多只有一個非負解,即圓與拋物線至多只有兩個交點,
不存在![]() ,使拋物線
,使拋物線![]() 的焦點恰為
的焦點恰為![]() 的外心;③不正確;
的外心;③不正確;
④![]() 的方程為
的方程為![]() ,代入拋物線方程得,
,代入拋物線方程得,
![]() ,
,
![]()
設![]() 中點
中點![]() ,
,![]() 軸,
軸,![]() ,
,
![]() ,代入拋物線方程得
,代入拋物線方程得
![]() ,
,
![]() .
.
④不正確.
故答案為:①②.


科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體中,正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,四邊形
,四邊形![]() 為平行四邊形,
為平行四邊形,![]() 為
為![]() 上一點,且
上一點,且![]() 平面
平面![]() ,
,![]() .
.
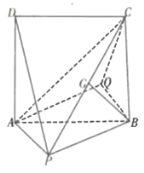
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 體積最大時,求直線
體積最大時,求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中
,其中![]() ,若
,若![]() 、
、![]() 、
、![]() 是
是![]() 的三條邊長,則下列結論:①對于一切
的三條邊長,則下列結論:①對于一切![]() 都有
都有![]() ;②存在
;②存在![]() 使
使![]() 、
、![]() 、
、![]() 不能構成一個三角形的三邊長;③
不能構成一個三角形的三邊長;③![]() 為鈍角三角形,存在
為鈍角三角形,存在![]() ,使
,使![]() ,其中正確的個數為______個
,其中正確的個數為______個
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三家企業產品的成本分別為10000,12000,15000,其成本構成如下圖所示,則關于這三家企業下列說法錯誤的是( )
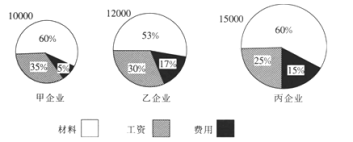
A.成本最大的企業是丙企業B.費用支出最高的企業是丙企業
C.支付工資最少的企業是乙企業D.材料成本最高的企業是丙企業
查看答案和解析>>
科目:高中數學 來源: 題型:
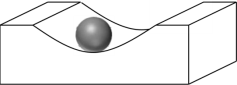
【題目】一個工業凹槽的軸截面是雙曲線的一部分,它的方程是![]() ,在凹槽內放入一個清潔鋼球(規則的球體),要求清潔鋼球能擦凈凹槽的最底部,則清潔鋼球的最大半徑為________.
,在凹槽內放入一個清潔鋼球(規則的球體),要求清潔鋼球能擦凈凹槽的最底部,則清潔鋼球的最大半徑為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市有東、西、南、北四個進入城區主干道的入口,在早高峰時間段,時常發生交通擁堵,交警部門記錄了11月份30天內的擁堵情況(如下表所示,其中●表示擁堵,○表示通暢).假設每個人口是否發生擁堵相互獨立,將各入口在這30天內擁堵的頻率代替各入口每天擁堵的概率.
11.1 | 11.2 | 11.3 | 11.4 | 11.5 | 11.6 | 11.7 | 11.8 | 11.9 | 11.10 | 11.11 | 11.12 | 11.13 | 11.14 | 11.15 | ||||||||||||||||
東入口 | ● | ○ | ○ | ○ | ○ | ● | ○ | ● | ● | ○ | ● | ● | ● | ○ | ● | |||||||||||||||
西入口 | ○ | ○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ● | ○ | ○ | |||||||||||||||
南入口 | ○ | ● | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ● | |||||||||||||||
北入口 | ● | ○ | ○ | ○ | ● | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ● | ○ | |||||||||||||||
11.16 | 11.17 | 11.18 | 11.19 | 11.20 | 11.21 | 11.22 | 11.23 | 11.24 | 11.25 | 11.26 | 11.27 | 11.28 | 11.29 | 11.30 | ||||||||||||||||
東入口 | ● | ○ | ○ | ● | ○ | ○ | p>○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | |||||||||||||||
西入口 | ● | ○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | |||||||||||||||
南入口 | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ● | |||||||||||||||
北入口 | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ● | ○ | |||||||||||||||
(1)分別求該城市一天中早高峰時間段這四個主干道的入口發生擁堵的概率.
(2)各人口一旦出現擁堵就需要交通協管員來疏通,聘請交通協管員有以下兩種方案可供選擇.方案一:四個主干道入口在早高峰時間段每天各聘請一位交通協管員,聘請每位交通協管員的日費用為![]() (
(![]() ,且
,且![]() )元.方案二:在早高峰時間段若某主干道入口發生擁堵,交警部門則需臨時調派兩位交通協管員協助疏通交通,調派后當日需給每位交通協管員的費用為200元.以四個主干道入口聘請交通協管員的日總費用的數學期望為依據,你認為在這兩個方案中應該如何選擇?請說明理由.
)元.方案二:在早高峰時間段若某主干道入口發生擁堵,交警部門則需臨時調派兩位交通協管員協助疏通交通,調派后當日需給每位交通協管員的費用為200元.以四個主干道入口聘請交通協管員的日總費用的數學期望為依據,你認為在這兩個方案中應該如何選擇?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,點
,點![]()
(1)求點![]() 與拋物線
與拋物線![]() 的焦點
的焦點![]() 的距離;
的距離;
(2)設斜率為![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,若
兩點,若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)是否存在定圓![]() ,使得過曲線
,使得過曲線![]() 上任意一點
上任意一點![]() 作圓
作圓![]() 的兩條切線,與曲線
的兩條切線,與曲線![]() 交于另外兩點
交于另外兩點![]() 時,總有直線
時,總有直線![]() 也與圓
也與圓![]() 相切?若存在,求出
相切?若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家每年都會對中小學生進行體質健康監測,一分鐘跳繩是監測的項目之一.今年某小學對本校六年級300名學生的一分鐘跳繩情況做了統計,發現一分鐘跳繩個數最低為10,最高為189.現將跳繩個數分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6組,并繪制出如下的頻率分布直方圖.
6組,并繪制出如下的頻率分布直方圖.
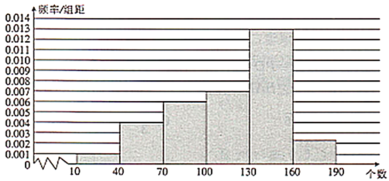
(1)若一分鐘跳繩個數達到160為優秀,求該校六年級學生一分鐘跳繩為優秀的人數;
(2)上級部門要對該校體質監測情況進行復查,發現每組男、女學生人數比例有很大差別,![]() 組男、女人數之比為
組男、女人數之比為![]() ,
,![]() 組男、女人數之比為
組男、女人數之比為![]() ,
,![]() 組男、女人數之比為
組男、女人數之比為![]() ,
,![]() 組男、女人數之比為
組男、女人數之比為![]() ,
,![]() 組男、女人數之比為
組男、女人數之比為![]() ,
,![]() 組男、女人數之比為
組男、女人數之比為![]() .試估計此校六年級男生一分鐘跳繩個數的平均數(同一組中的數據用該組區間的中點值作代表,結果保留整數).
.試估計此校六年級男生一分鐘跳繩個數的平均數(同一組中的數據用該組區間的中點值作代表,結果保留整數).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com