
���}Ŀ��ƽ��ֱ������(bi��o)ϵ![]() �У��E�AC��
���E�AC��![]() ���x������
���x������![]() �����タE��
�����タE��![]() �Ľ��c(di��n)F��C��һ����c(di��n)��
�Ľ��c(di��n)F��C��һ����c(di��n)��
��������E�AC�ķ��̣�
�������O(sh��)P��E�ϵĄ��c(di��n)����λ�ڵ�һ���ޣ�E���c(di��n)P̎���о�![]() �cC���c��ͬ�ă��c(di��n)A��B������AB�����c(di��n)��D��ֱ��OD�c�^P�Ҵ�ֱ��x�S��ֱ�������c(di��n)M��
�cC���c��ͬ�ă��c(di��n)A��B������AB�����c(di��n)��D��ֱ��OD�c�^P�Ҵ�ֱ��x�S��ֱ�������c(di��n)M��
��i�����C���c(di��n)M�ڶ�ֱ����;
��ii��ֱ��![]() �cy�S�����c(di��n)G��ӛ
�cy�S�����c(di��n)G��ӛ![]() ����e��
����e��![]() ��
��![]() ����e��
����e��![]() ����
����![]() �����ֵ��ȡ�����ֵ�r�c(di��n)P������(bi��o)��
�����ֵ��ȡ�����ֵ�r�c(di��n)P������(bi��o)��
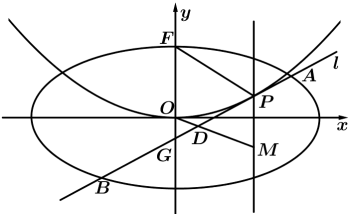
���𰸡�������![]() ;������������Ҋ������������
;������������Ҋ������������![]() �����ֵ��
�����ֵ��![]() ���˕r�c(di��n)
���˕r�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]()
��������
ԇ�}����������(j��)�E�A���x���ʺͽ��c(di��n)�̣�
���������������c(di��n)P������(bi��o)��б���O(sh��)��ֱ��l�ķ��̺͒��タ(li��n)�����M(j��n)���Д��c(di��n)M�ڶ�ֱ���ϣ�
�������քe�г�![]() ��
��![]() ��e�ı��_(d��)ʽ������(j��)���κ���(sh��)����ֵ�ʹ˕r�c(di��n)P������(bi��o)��
��e�ı��_(d��)ʽ������(j��)���κ���(sh��)����ֵ�ʹ˕r�c(di��n)P������(bi��o)��
ԇ�}���������������}��֪��![]() �����
�����![]() ��
��
��?y��n)钁�タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ������
������![]() ��
��
���ԙE�A�ķ��̞�![]() ��
��
��������1���O(sh��)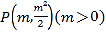 ����
����![]() �ɵ�
�ɵ�![]() ��
��
����ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ����ֱ�����̞�
����ֱ�����̞�![]() ����
����![]() ��
��
�O(sh��)![]() ��(li��n)�����̽M
��(li��n)�����̽M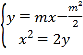
��ȥ![]() �������ɵ�
�������ɵ�![]() ��
��
�������Єeʽ![]() �ɵ�
�ɵ�![]() ��
��![]() ��
��
��![]() ,
,
����![]() �ɵ�
�ɵ�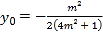 ��
��
��?y��n)?/span>![]() ������ֱ��
������ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
(li��n)�� �ɵ��c(di��n)
�ɵ��c(di��n)![]() �Ŀv����(bi��o)��
�Ŀv����(bi��o)��![]() �����c(di��n)
�����c(di��n)![]() �ڶ�ֱ��
�ڶ�ֱ��![]() �ϣ�
�ϣ�
��2���ɣ�1��ֱ֪��![]() �ķ��̞�
�ķ��̞�![]() ��
��
��![]() ��
��![]() ������
������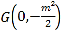 ��
��
��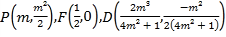 ��
��
����![]() ��
��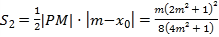 ��
��
����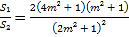 ����
����![]() ���t
���t![]() ��
��
��ˮ�(d��ng)![]() ����
����![]() �r��
�r��![]() ��������ֵ��
��������ֵ��![]() ���˕r
���˕r![]() �M��
�M��![]() ��
��
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��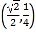 �����
�����![]() �����ֵ��
�����ֵ��![]() ���˕r�c(di��n)
���˕r�c(di��n)![]() ������(bi��o)��
������(bi��o)��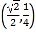 ��
��


 �ʐ�Ӣ�Zͬ������(x��)��ϵ�д�
�ʐ�Ӣ�Zͬ������(x��)��ϵ�д� �W(xu��)��(x��)��(sh��)�`�@��ϵ�д�
�W(xu��)��(x��)��(sh��)�`�@��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪������ABCD��,E,F�քe��CD,AD�����c(di��n),BE,CF�����c(di��n)P.���C��

��1��BE��CF;
��2��AP=AB.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��(1)���cֱ��3x��4y��7��0��ֱ�����cԭ�c(di��n)�ľ��x��6��ֱ�����̣�
(2)��(j��ng)�^ֱ��l1��2x��3y��5��0�cl2��7x��15y��1��0�Ľ��c(di��n)����ƽ����ֱ��x��2y��3��0��ֱ�����̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��[�x��4��4������(bi��o)ϵ�c����(sh��)����]
��ֱ������(bi��o)ϵ![]() �У�����
�У�����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����ֱ��
�酢��(sh��)����ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)��.
�酢��(sh��)��.
��1����![]() ��
��![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2��������![]() ��ֱ��
��ֱ��![]() ���þ��ε����c(di��n)����(bi��o)��
���þ��ε����c(di��n)����(bi��o)��![]() ����
����![]() ��б�ʣ�
��б�ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() ���x����
���x����![]() ���^�E�A�����c(di��n)
���^�E�A�����c(di��n)![]() �҃Aб�Ǟ�
�҃Aб�Ǟ�![]() ��ֱ���c�A
��ֱ���c�A![]() �ཻ�������L��
�ཻ�������L��![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���Ƿ�����^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ���c(di��n)����
���c(di��n)����![]() �������ڣ���ֱ��
�������ڣ���ֱ��![]() �ķ��̣��������ڣ��f�����ɣ�
�ķ��̣��������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �Ķ��x��?y��n)?/span>
�Ķ��x��?y��n)?/span>![]() ���Ҵ��ڌ�(sh��)����(sh��)
���Ҵ��ڌ�(sh��)����(sh��)![]() ��ʹ�Ì��ڶ��x���(n��i)����
��ʹ�Ì��ڶ��x���(n��i)����![]() ������
������![]() �������t�Q�˺���(sh��)
�������t�Q�˺���(sh��)![]() ���������|(zh��)
���������|(zh��)![]() ��
��
��1���Дຯ��(sh��)![]() �Ƿ������
�Ƿ������![]() ���|(zh��)������������
���|(zh��)������������![]() ���|(zh��)�����t���
���|(zh��)�����t���![]() ��ֵ������������
��ֵ������������![]() ���|(zh��)����Ո�f�����ɣ�
���|(zh��)����Ո�f�����ɣ�
��2����֪����(sh��)![]() ������
������![]() ���|(zh��)���Һ���(sh��)
���|(zh��)���Һ���(sh��)![]() ��
��![]() �ϵ���Сֵ��
�ϵ���Сֵ��![]() ����(d��ng)
����(d��ng)![]() �r��
�r��![]() ����(sh��)
����(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() �ϵ�ֵ��
�ϵ�ֵ��
��3����֪����(sh��)![]() �Ⱦ�����
�Ⱦ�����![]() ���|(zh��)�����־�����
���|(zh��)�����־�����![]() ���|(zh��)�����Ү�(d��ng)
���|(zh��)�����Ү�(d��ng)![]() �r��
�r��![]() ��������(sh��)
��������(sh��)![]() ����
����![]() ǡ�ô���
ǡ�ô���![]() �����c(di��n)����
�����c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() ���A
���A![]() .
.
��1����ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() �ұ��A
�ұ��A![]() �صõľ����L��
�صõľ����L��![]() ����
����![]() �ķ��̣�
�ķ��̣�
��2�����^![]() �c(di��n)�ĈA
�c(di��n)�ĈA![]() ���ҵ����c(di��n)
���ҵ����c(di��n)![]() ��܉�E����.
��܉�E����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() �����������Ğ������c(di��n)E�ǂ�(c��)��
�����������Ğ������c(di��n)E�ǂ�(c��)��![]() �ϵ�һ�����c(di��n)���������Дࣺ
�ϵ�һ�����c(di��n)���������Дࣺ

��ֱ��AC�cֱ��![]() �Ǯ���ֱ����
�Ǯ���ֱ����
��![]() һ������ֱ
һ������ֱ![]() ��
��
�������F![]() ���w�e�鶨ֵ��
���w�e�鶨ֵ��
��![]() ����Сֵ��
����Сֵ��![]()
��ƽ��![]() �cƽ��
�cƽ��![]() ���ɽǞ�
���ɽǞ�![]()
�������_����̖��_______
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(j��ng)�{(di��o)�飬3���������о���һ����Ѫ������ôʲô�Ǹ�Ѫ����Ѫ�������������ģ���(j��ng)���H�l(w��i)���M����������ͬ���g����Ⱥ�M(j��n)��Ѫ���{(di��o)�飬�ó��S���g׃�����տs��������ֵ׃����r���±���

���� 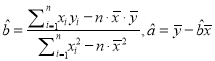 ��
�� ![]() ��
�� ![]()
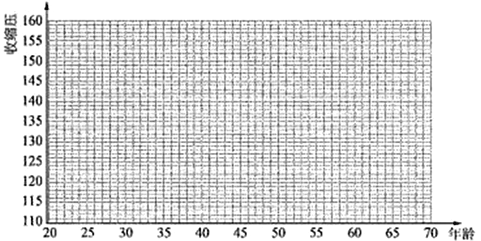
��1��Ո�����ϱ픵(sh��)��(j��)��ɢ�c(di��n)�D��
��2��Ո����(j��)�ϱ��ṩ�Ĕ�(sh��)��(j��)������С���˷����![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw����
�ľ��Իؚw����![]() ����
����![]() ��ֵ���_��0.01��
��ֵ���_��0.01��
��3����Ҏ(gu��)����һ���˵��տs�����(bi��o)��(zh��n)ֵ��0.9~1.06�����t��Ѫ��������Ⱥ���տs�����(bi��o)��(zh��n)ֵ��1.06~1.12�����t���p�ȸ�Ѫ����Ⱥ���տs�����(bi��o)��(zh��n)ֵ��1.12~1.20�����t���жȸ�Ѫ����Ⱥ���տs�����(bi��o)��(zh��n)ֵ��1.20�������ϣ��t��߶ȸ�Ѫ����Ⱥ.һλ�տs����180mmHg��70�q�����ˣ����������Ⱥ��
���𰸡�(1)��Ҋ������(2) ![]() ��(3)�жȸ�Ѫ����Ⱥ.
��(3)�жȸ�Ѫ����Ⱥ.
��������ԇ�}��������1������(sh��)��(j��)����(y��ng)���c(di��n)������ɢ�c(di��n)�D����2�������ֵ���ٴ��˹�ʽ��![]() ������
������![]() ��
��![]() ����3������(j��)�ؚwֱ����������׃����180�r����(y��ng)����(sh��)ֵ�������c��(bi��o)��(zh��n)ֵ�ı���(sh��)���_��������Ⱥ.
����3������(j��)�ؚwֱ����������׃����180�r����(y��ng)����(sh��)ֵ�������c��(bi��o)��(zh��n)ֵ�ı���(sh��)���_��������Ⱥ.
ԇ�}������(1) 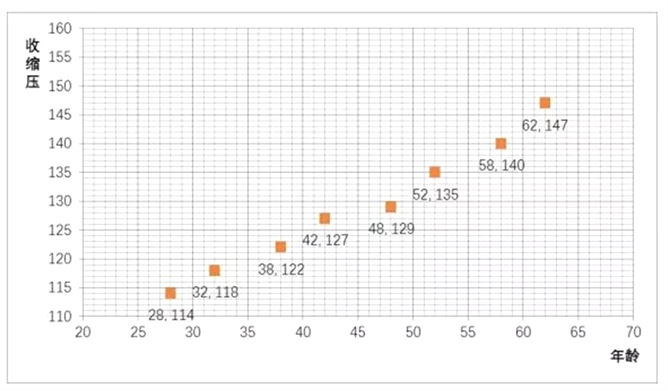
��2��![]()
![]()
��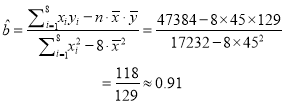
![]()
��ؚwֱ�����̞�![]() .
.
��3������(j��)�ؚwֱ�����̵��A(y��)�y�����g��70�q�����˘�(bi��o)��(zh��n)�տs���s��![]() ��mmHg����
��mmHg����![]()
���տs����180mmHg��70�q���˞��жȸ�Ѫ����Ⱥ.
���}�͡�����}
���Y(ji��)����
19
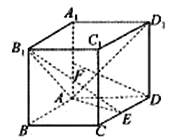
���}Ŀ����D��������![]() �ĵ�������Σ�
�ĵ�������Σ� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ���c(di��n).
���c(di��n).
��1�����C�� ![]() ƽ��
ƽ��![]() ��
��
��2����![]() ����
����![]() ����ֱ��
����ֱ��![]() �cƽ��
�cƽ��![]() ���ɾ���ǵ�����ֵ��
���ɾ���ǵ�����ֵ��![]() ����
����![]() ���L.
���L.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com