
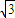 y+2=0的傾斜角范圍是( )
y+2=0的傾斜角范圍是( )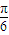 ,
,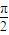 )∪(
)∪(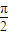 ,]
,]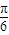 ]∪[
]∪[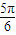 ,π)
,π)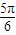 ]
]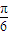 ,
,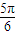 ]
]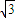 y+2=0,我們不難得到直線的斜率的表達式,結合三角函數的性質,不得得到斜率的取值范圍,再根據斜率與傾斜角的關系,進一步可以得到傾斜角的取值范圍.
y+2=0,我們不難得到直線的斜率的表達式,結合三角函數的性質,不得得到斜率的取值范圍,再根據斜率與傾斜角的關系,進一步可以得到傾斜角的取值范圍. cosα.
cosα.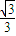 ≤tanθ≤
≤tanθ≤ .
. ]∪[
]∪[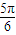 ,π).
,π).

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com