
【題目】已知數列{an}的前n項和Sn=k3n﹣m,且a1=3,a3=27.
(I)求證:數列{an}是等比數列;
(II)若anbn=log3an+1 , 求數列{bn}的前n項和Tn .
【答案】證明:(I)∵ ![]() ,∴S1=a1=3k﹣m=3,a3=S3﹣S2=18k=27,解得
,∴S1=a1=3k﹣m=3,a3=S3﹣S2=18k=27,解得 ![]() .
.
則當n≥2時, ![]() ,
,
又a1=3,∴n∈N* , ![]() .
.
則 ![]() 為常數,故由等比數列的定義可知,數列{an}是等比數列.
為常數,故由等比數列的定義可知,數列{an}是等比數列.
(II)解:∵anbn=log3an+1 , ∴ ![]() .
.
則 ![]() ,
,
∴ ![]() ,
,
則 ![]() ,
,
即 ![]() (n∈N*)
(n∈N*)
【解析】(I)利用遞推關系與等比數列的定義即可證明.(II)利用“錯位相減法”、等比數列的求和公式即可得出.
【考點精析】關于本題考查的等比關系的確定和數列的前n項和,需要了解等比數列可以通過定義法、中項法、通項公式法、前n項和法進行判斷;數列{an}的前n項和sn與通項an的關系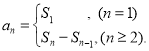 才能得出正確答案.
才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若關于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8個不同的實數根,則b+c的取值范圍為( )
,若關于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8個不同的實數根,則b+c的取值范圍為( )
A.(﹣∞,3)
B.(0,3]
C.[0,3]
D.(0,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,⊙O是以AB為直徑的圓,點C在圓上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延長線與AB的延長線交于點E.若EB=6,EC=6 ![]() ,則BC的長為 .
,則BC的長為 . 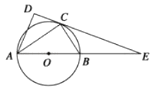
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有4個人去參加某娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇.為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲,擲出點數為1或2的人去參加甲游戲,擲出點數大于2的人去參加乙游戲.
(Ⅰ)求這4個人中恰有2人去參加甲游戲的概率;
(Ⅱ)用X,Y分別表示這4個人中去參加甲、乙游戲的人數,記ξ=|X﹣Y|,求隨機變量ξ的分布列與數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某測試中,卷面滿分為100分,60分為及格,為了調查午休對本次測試前兩個月復習效果的影響,特對復習中進行午休和不進行午休的考生進行了測試成績的統計,數據如下表所示:
分數段 | 29~ 40 | 41~ 50 | 51~ 60 | 61~ 70 | 71~ 80 | 81~ 90 | 91~ 100 |
午休考 生人數 | 23 | 47 | 30 | 21 | 14 | 31 | 14 |
不午休 考生人數 | 17 | 51 | 67 | 15 | 30 | 17 | 3 |
(1)根據上述表格完成列聯表:
及格人數 | 不及格人數 | 總計 | |
午休 | |||
不午休 | |||
總計 |
(2)根據列聯表可以得出什么樣的結論?對今后的復習有什么指導意義?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學城校區與本部校區之間的駕車單程所需時間為![]() ,
,![]() 只與道路暢通狀況有關,對其容量為500的樣本進行統計,結果如下:
只與道路暢通狀況有關,對其容量為500的樣本進行統計,結果如下:
| 25 | 30 | 35 | 40 |
頻數(次) | 100 | 150 | 200 | 50 |
以這500次駕車單程所需時間的頻率代替某人1次駕車單程所需時間的概率.
(1)求![]() 的分布列與
的分布列與![]() ;
;
(2)某天有3位教師獨自駕車從大學城校區返回本部校區,記![]() 表示這3位教師中駕車所用時間少于
表示這3位教師中駕車所用時間少于![]() 的人數,求
的人數,求![]() 的分布列與
的分布列與![]() ;
;
(3)下周某天張老師將駕車從大學城校區出發,前往本部校區做一個50分鐘的講座,結束后立即返回大學城校區,求張老師從離開大學城校區到返回大學城校區共用時間不超過120分鐘的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣…+
﹣…+ ![]() ﹣
﹣ ![]() +
+ ![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A.f(x)在(0,1)上恰有一個零點
B.f(x)在(0,1)上恰有兩個零點
C.f(x)在(﹣1,0)上恰有一個零點
D.f(x)在(﹣1,0)上恰有兩個零點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系原點O為極點,以x軸非負半軸為極軸,以平面直角坐標系的長度單位為長度單位建立極坐標系.已知直線l的參數方程為 ![]() (t為參數),曲線C的極坐標方程為ρsin2θ=4cosθ
(t為參數),曲線C的極坐標方程為ρsin2θ=4cosθ
(Ⅰ) 求曲線C的直角坐標方程;
(Ⅱ) 設直線l與曲線C相交于A,B兩點,求|AB|.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com