
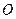 的方程為
的方程為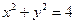 .
.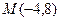 的圓
的圓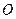 的切線方程;
的切線方程;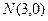 作直線與圓
作直線與圓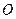 交于
交于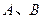 兩點,求
兩點,求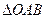 的最大面積以及此時直線
的最大面積以及此時直線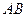 的斜率.
的斜率.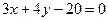 或
或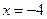 .
.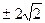
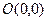 ,半徑
,半徑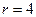
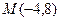 的切方程為
的切方程為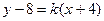 ,即
,即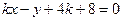 , ----------------1分
, ----------------1分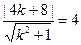 ,解得
,解得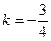 ----------------3分
----------------3分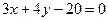 ----------------5分
----------------5分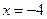 也符合題意.
也符合題意.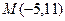 的圓
的圓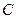 的切線方程為:
的切線方程為: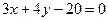 或
或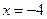 . --------------6分
. --------------6分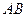 的斜率不存在時,
的斜率不存在時,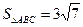 , ----------------------------7分
, ----------------------------7分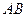 的斜率存在時,設直線
的斜率存在時,設直線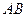 的方程為
的方程為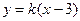 ,即
,即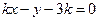 ,
,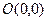 到直線
到直線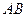 的
的 距離
距離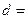
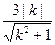 , ----------------9分
, ----------------9分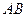 的長度
的長度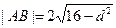 ,
,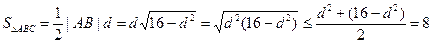 -------------11分
-------------11分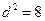 時取等號,此時
時取等號,此時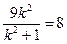 ,解得
,解得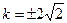
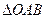 的最大面積為8,此時直線
的最大面積為8,此時直線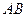 的斜率為
的斜率為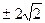 . ------------
. ------------ ----12分
----12分

 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com