
【題目】已知函數 ![]() ,把方程f(x)=x的根按從小到大的順序排列成一個數列,則該數列的通項公式為( )
,把方程f(x)=x的根按從小到大的順序排列成一個數列,則該數列的通項公式為( )
A.![]() (n∈N*)
(n∈N*)
B.an=n(n﹣1)(n∈N*)
C.an=n﹣1(n∈N*)
D.an=2n﹣2(n∈N*)
【答案】C
【解析】解:若0<x≤1,則﹣1<x﹣1<0,得f(x)=f(x﹣1)+1=2x﹣1 , 若1<x≤2,則0<x﹣1≤1,得f(x)=f(x﹣1)+1=2x﹣2+1
若2<x≤3,則1<x﹣1≤2,得f(x)=f(x﹣1)+1=2x﹣3+2
若3<x≤4,則2<x﹣1<3,得f(x)=f(x﹣1)+1=2x﹣4+3
以此類推,若n<x≤n+1(其中n∈N),則f(x)=f(x﹣1)+1=2x﹣n﹣1+n,
下面分析函數f(x)=2x的圖象與直線y=x+1的交點
很顯然,它們有兩個交點(0,1)和(1,2),
由于指數函數f(x)=2x為增函數且圖象下凸,故它們只有這兩個交點.
然后①將函數f(x)=2x和y=x+1的圖象同時向下平移一個單位即得到函數f(x)=2x﹣1和y=x的圖象,
取x≤0的部分,可見它們有且僅有一個交點(0,0).
即當x≤0時,方程f(x)﹣x=0有且僅有一個根x=0.
②取①中函數f(x)=2x﹣1和y=x圖象﹣1<x≤0的部分,再同時向上和向右各平移一個單位,
即得f(x)=2x﹣1和y=x在0<x≤1上的圖象,顯然,此時它們仍然只有一個交點(1,1).
即當0<x≤1時,方程f(x)﹣x=0有且僅有一個根x=1.
③取②中函數f(x)=2x﹣1和y=x在0<x≤1上的圖象,繼續按照上述步驟進行,
即得到f(x)=2x﹣2+1和y=x在1<x≤2上的圖象,顯然,此時它們仍然只有一個交點(2,2).
即當1<x≤2時,方程f(x)﹣x=0有且僅有一個根x=2.
④以此類推,函數y=f(x)與y=x在(2,3],(3,4],…(n,n+1]上的交點依次為(3,3),(4,4),…(n+1,n+1).
即方程f(x)﹣x=0在(2,3],(3,4],…(n,n+1]上的根依次為3,4,…n+1.
綜上所述方程f(x)﹣x=0的根按從小到大的順序排列所得數列為
0,1,2,3,4,…
其通項公式為an=n﹣1;
故選C.
【考點精析】本題主要考查了數列的通項公式的相關知識點,需要掌握如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 已知2Sn=3n+3.
(Ⅰ)求{an}的通項公式;
(Ⅱ)若數列{bn},滿足anbn=log3an , 求{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() (x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f[g(2)]的值;
(3)求f[g(x)]和g[f(x)]的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
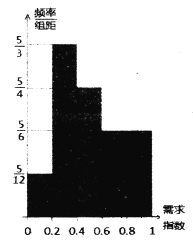
【題目】某公司每個工作日由位于市區的總公司向位于郊區的分公司開一個來回的班車(每年按200個工作日計算),現有兩種使用班車的方案,方案一是購買一輛大巴,需花費90萬元,報廢期為10年,車輛平均每年的各種費用合計5萬元,司機年工資6萬元,司機每天請假的概率為0.1(每年請假時間不超過15天不扣工資,超過15天每天100元),若司機請假則需從公交公司雇傭司機,每天支付300元工資.方案二是租用公交公司的車輛(含司機),根據調研每年12個月的車輛需求指數如直方圖所示,其中當某月車輛需求指數在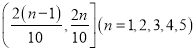 時,月租金為
時,月租金為![]() 萬元.
萬元.
(1)若購買大巴,設司機每年請假天數為![]() ,求公司因司機請假而增加的花費
,求公司因司機請假而增加的花費![]() (元)及使用班車年平均花費
(元)及使用班車年平均花費![]() (萬元)的數學期望
(萬元)的數學期望![]() .
.
(2)試用調研數據,給出公司使用班車的建議,使得年平均花費最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=x+ ![]() (a>0)在區間
(a>0)在區間 ![]() 上單調遞減,在區間
上單調遞減,在區間 ![]() 上單調遞增;函數
上單調遞增;函數 ![]()
(1)請寫出函數f(x)=x2+ ![]() (a>0)與函數g(x)=xn+
(a>0)與函數g(x)=xn+ ![]() (a>0,n∈N,n≥3)在(0,+∞)的單調區間(只寫結論,不證明);
(a>0,n∈N,n≥3)在(0,+∞)的單調區間(只寫結論,不證明);
(2)求函數h(x)的最值;
(3)討論方程h2(x)﹣3mh(x)+2m2=0(0<m≤30)實根的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是R上的偶函數,對于任意x∈R,都有f(x+6)=f(x)+f(3)成立,當x1 , x2∈[0,3],且x1≠x2時,都有 ![]() .給出下列命題: ①f(3)=0;
.給出下列命題: ①f(3)=0;
②直線x=﹣6是函數y=f(x)的圖象的一條對稱軸;
③函數y=f(x)在[﹣9,﹣6]上為增函數;
④函數y=f(x)在[﹣9,9]上有四個零點.
其中所有正確命題的序號為(把所有正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 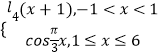 ,若存在實數x1 , x2 , x3 , x4 , 滿足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),則
,若存在實數x1 , x2 , x3 , x4 , 滿足x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),則 ![]() 的取值范圍是( ).
的取值范圍是( ).
A.(0,4)
B.(0, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在五面體ABCDEF中,四邊形ABCD是邊長為2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() ,H是BC的中點.
,H是BC的中點. 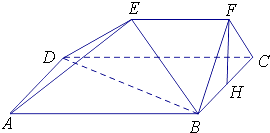
(1)求證:FH∥平面BDE;
(2)求證:AB⊥平面BCF;
(3)求五面體ABCDEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)是定義在R上的偶函數,且對任意的x∈R恒有f(x+1)=f(x-1),
已知當x∈[0,1]時f(x)=(![]() )1-x,則
)1-x,則
①2是函數f(x)的周期;
②函數f(x)在(1,2)上是減函數,在(2,3)上是增函數;
③函數f(x)的最大值是1,最小值是0;
④當x∈(3,4)時,f(x)=(![]() )x-3.
)x-3.
其中所有正確命題的序號是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com