【題目】已兩動圓
和
，把它們的公共點的軌跡記為曲線
，若曲線與
軸的正半軸交點為
，且曲線上異于點的相異兩點
、
滿足
.
(1)求曲線的方程；
(2)證明直線
恒經過一定點，并求出此定點的坐標.
【答案】（1）
；（2）直線
恒過定點
。
【解析】
（1）設兩動圓的公共點為
，則有
，運用橢圓的定義，即可得到
，
，
，進而得到的軌跡方程；
（2）
，設
，
，
，
，根據直線的斜率不存在和存在，設出直線方程，根據條件，運用向量的數量積的坐標表示，結合韋達定理和直線恒過定點的求法，即可得到定點；
解：（1）設兩動圓的公共點為，則有
．
由橢圓的定義可知的軌跡是以
、
為焦點橢圓，且
．
，
所以曲線
的方程是：．
（2）證明：由題意可知：，設，，，，
當的斜率不存在時，易知滿足條件
的直線為：
，過定點；
當的斜率存在時，設直線
，聯立方程組：
，
把②代入①有：
，
③，
④，
因為，所以有
即
，
，
把③④代入整理：
，
（有公因式
繼續化簡得
，
或
（舍去
，
綜上，直線恒過定點．
閱讀快車系列答案科目：高中數學 來源： 題型：
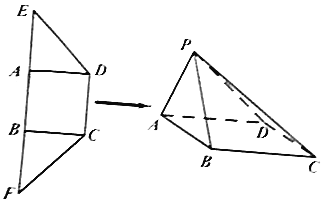
【題目】如圖所示，在梯形CDEF中，四邊形ABCD為正方形，且
，將
沿著線段AD折起，同時將
沿著線段BC折起，使得E，F兩點重合為點P．
求證：平面
平面ABCD；
求直線PB與平面PCD的所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知偶函數
滿足
，現給出下列命題：①函數是以2為周期的周期函數；②函數是以4為周期的周期函數；③函數
為奇函數；④函數
為偶函數，則其中真命題的個數是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標平面上的一列點
簡記為
，若由
構成的數列
滿足
，（其中
是與
軸正方向相同的單位向量），則稱為“
點列”.
（1）試判斷：
，...是否為“點列”？并說明理由.
（2）若為“點列”，且點
在點
的右上方.任取其中連續三點
，判斷
的形狀（銳角，直角，鈍角三角形），并證明.
（3）若為“點列”，正整數
滿足：
，且
，求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知偶函數滿足，現給出下列命題：①函數是以2為周期的周期函數；②函數是以4為周期的周期函數；③函數為奇函數；④函數為偶函數，則其中真命題的個數是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某游戲廠商對新出品的一款游戲設定了“防沉迷系統”，規則如下：
①3小時以內(含3小時)為健康時間，玩家在這段時間內獲得的累積經驗值
單位：
與游玩時間
小時)滿足關系式：
；
②3到5小時(含5小時)為疲勞時間，玩家在這段時間內獲得的經驗值為
即累積經驗值不變)；
③超過5小時為不健康時間，累積經驗值開始損失，損失的經驗值與不健康時間成正比例關系，比例系數為50．
⑴當
時，寫出累積經驗值E與游玩時間t的函數關系式
，并求出游玩6小時的累積經驗值；
⑵該游戲廠商把累積經驗值E與游玩時間t的比值稱為“玩家愉悅指數”，記作
；若
，且該游戲廠商希望在健康時間內，這款游戲的“玩家愉悅指數”不低于24，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
