
【題目】某房地產開發商為吸引更多消費者購房,決定在一塊閑置的扇形空地中修建一個花園.如圖,已知扇形AOB的圓心角∠AOB=![]() ,半徑為R.現欲修建的花園為OMNH,其中M,H分別在OA,OB上,N在
,半徑為R.現欲修建的花園為OMNH,其中M,H分別在OA,OB上,N在![]() 上.設∠MON=θ,OMNH的面積為S.
上.設∠MON=θ,OMNH的面積為S.

(1)將S表示為關于θ的函數;
(2)求S的最大值及相應的θ值.
【答案】(1)S=R2(cos θ-sin θ)sin θ,θ∈![]() ;(2)θ=
;(2)θ=![]() 時,S取得最大值
時,S取得最大值![]() R2.
R2.
【解析】
(1)分別過N,H作ND⊥OA于D,HE⊥OA于E,則HEDN為矩形,求出邊長,即可求S關于θ的函數關系式;(2)利用二倍角公式、兩角和的正弦函數化簡函數的表達式為一個角的一個三角函數的形式,通過θ的范圍求出S的最大值及相應的θ角.
(1)如圖,過N作NP⊥OA于點P,過H作HE⊥OA于點E,∵∠AOB=![]() ,
,
∴OE=EH=NP=Rsin θ,OP=Rcos θ,
∴HN=EP=OP-OE=R(cos θ-sin θ),
∴S=HN·NP=R2(cos θ-sin θ)sin θ,θ∈![]() .
.
(2)S=R2(cos θsin θ-sin2θ)
=R2![]()
=![]() R2(sin 2θ+cos 2θ-1)
R2(sin 2θ+cos 2θ-1)
=![]() R2
R2![]() ,
,
∵θ∈![]() ,∴2θ+
,∴2θ+![]() ,
,
∴當2θ+![]() ,即θ=
,即θ=![]() 時,S取得最大值,且最大值為
時,S取得最大值,且最大值為![]() R2.
R2.


科目:高中數學 來源: 題型:
【題目】
袋中有形狀和大小完全相同的四種不同顏色的小球,每種顏色的小球各有4個,分別編號為1,2,3,4.現從袋中隨機取兩個球.
(Ⅰ)若兩個球顏色不同,求不同取法的種數;
(Ⅱ)在(1)的條件下,記兩球編號的差的絕對值為隨機變量X,求隨機變量X的概率分布與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的三棱錐ABC﹣A1B1C1中,AA1⊥底面ABC,D,E分別是BC,A1B1的中點. 
(1)求證:DE∥平面ACC1A1;
(2)若AB⊥BC,AB=BC,∠ACB1=60°,求直線BC與平面AB1C所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的可導函數f(x)滿足f′(x)+f(x)<0,設a=f(m﹣m2),b=e ![]() f(1),則a,b的大小關系是( )
f(1),則a,b的大小關系是( )
A.a>b
B.a<b
C.a=b
D.a,b的大小與m的值有關
查看答案和解析>>
科目:高中數學 來源: 題型:
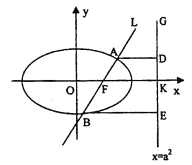
【題目】如圖,已知直線![]() 的右焦點
的右焦點![]() ,且交橢圓
,且交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 上的射影依次為點
上的射影依次為點![]() .
.
(Ⅰ)已知拋物線![]() 的焦點為橢圓
的焦點為橢圓![]() 的上頂點。
的上頂點。
①求橢圓![]() 的方程;
的方程;
②若直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() ,當
,當![]() 變化時,求
變化時,求![]() 的值;
的值;
(Ⅱ)連接![]() ,試探索當
,試探索當![]() 變化時,直線
變化時,直線![]() 是否相交于一定點
是否相交于一定點![]() ?若交于定點
?若交于定點![]() ,請求出
,請求出![]() 點的坐標并給予證明;否則說明理由.
點的坐標并給予證明;否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C的參數方程 ![]() (φ為參數),以O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數),以O為極點,x軸的非負半軸為極軸建立極坐標系.
(1)求圓C的極坐標方程;
(2)直線l的極坐標方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射線OM:θ=
,射線OM:θ= ![]() 與圓C的交點為O、P,與直線l的交點為Q,求線段PQ的長.
與圓C的交點為O、P,與直線l的交點為Q,求線段PQ的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com