
已知二項式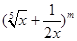 的展開式中第2項為常數項
的展開式中第2項為常數項 ,其中
,其中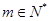 ,且展開式按
,且展開式按 的降冪排列.
的降冪排列.
(1)求 及
及 的值.
的值.
(2)數列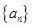 中,
中, ,
,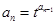 ,
,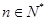 ,求證:
,求證: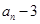 能被4整除.
能被4整除.
(1)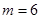 ,
,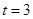 ;(2))證明過程詳見解析.
;(2))證明過程詳見解析.
解析試題分析:(1)由展開式中第2項為常數項,則可根據二項式展開式的第2項展開式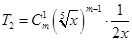 中未知數
中未知數 的指數為0,從而求出
的指數為0,從而求出 的值,將
的值,將 的值代回第2項展式可求出
的值代回第2項展式可求出 的值;(2)可利用數學歸納法來證明,①當
的值;(2)可利用數學歸納法來證明,①當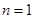 時,
時,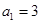 ,
,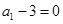 ,能被4整除,顯然命題成立;②假設當n=k時,
,能被4整除,顯然命題成立;②假設當n=k時,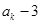 能被4整除,即
能被4整除,即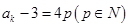 .那么當n =k+1時,
.那么當n =k+1時,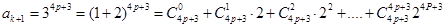
=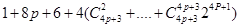 =
=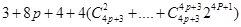
=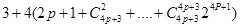 顯然
顯然 是非負整數,
是非負整數,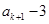 能被4整除.
能被4整除.
由①、②可知,命題對一切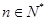 都成立.
都成立.
試題解析:(1) 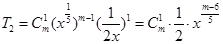 , 2分
, 2分
故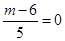 ,
,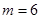 ,
,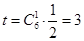 . 4分
. 4分
(2)證明:①當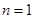 時,
時,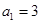 ,
,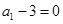 ,能被4整除.
,能被4整除.
②假設當n=k時,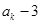 能被4整除,即
能被4整除,即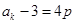 ,其中p是非負整數.
,其中p是非負整數.
那么當n =k+1時,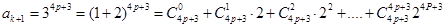
=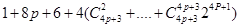 =
=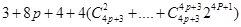
=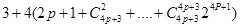 顯然
顯然 是非負整數,
是非負整數,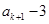 能被4整除.
能被4整除.
由①、②可知,命題對一切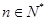 都成立. 10分
都成立. 10分
考點:1.二項式定理;2.數學歸納法.


科目:高中數學 來源: 題型:解答題
已知(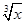 +x2)2n的展開式的二項式系數和比(3x-1)n的展開式的二項式系數和大992,求(2x-
+x2)2n的展開式的二項式系數和比(3x-1)n的展開式的二項式系數和大992,求(2x-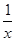 )2n的展開式中:
)2n的展開式中:
(1)二項式系數最大的項;
(2)系數的絕對值最大的項.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩人參加某種選拔測試.在備選的10道題中,甲答對其中每道題的概率都是 ,乙能答對其中5道題.規定每次考試都從備選的10道題中隨機抽出3道題進行測試,答對一題加10分,答錯一題(不答視為答錯)減5分,至少得15分才能入選.
,乙能答對其中5道題.規定每次考試都從備選的10道題中隨機抽出3道題進行測試,答對一題加10分,答錯一題(不答視為答錯)減5分,至少得15分才能入選.
(1)求乙得分的分布列和數學期望;
(2)求甲、乙兩人中至少有一人入選的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有8張卡片分別標有數字1,2,3,4,5,6,7,8,從中取出6張卡片排成3行2列,要求3行中僅有中間行的兩張卡片上的數字之和為5,則不同的排法共有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在產品質量檢驗時,常從產品中抽出一部分進行檢查.現在從98件正品和2件次品共100件產品中,任意抽出3件檢查.
(1)共有多少種不同的抽法?
(2)恰好有一件是次品的抽法有多少種?
(3)至少有一件是次品的抽法有多少種?
(4)恰好有一件是次品,再把抽出的3件產品放在展臺上,排成一排進行對比展覽,共有多少種不同的排法?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從5名女同學和4名男同學中選出4人參加演講比賽,分別按下列要求,各有多少種不同的選法?
(1)男、女同學各2名;
(2)男、女同學分別至少有1名;
(3)在(2)的前提下,男同學甲與女同學乙不能同時選出.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知甲、乙、丙等6人 .
(1)這6人同時參加一項活動,必須有人去,去幾人自行決定,共有多少種不同的去法?
(2)這6人同時參加6項不同的活動,每項活動限1人參加,其中甲不參加第一項活動,乙不參加第三項活動,共有多少種不同的安排方法?
(3)這6人同時參加4項不同的活動,求每項活動至少有1人參加的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com