設f(x)=ax2+(b-8)x-a-ab,不等式f(x)>0的解集是(-3,2).
(1)求f(x);
(2)當函數f(x)的定義域是[0,1]時,求函數f(x)的值域.
【答案】
分析:(1)由不等式f(x)>0的解集是(-3,2),結合函數零點、方程的根與不等式解集的端點之間的關系,我們易得到-3,2是方程ax
2+(b-8)x-a-ab=0的兩個根,根據韋達定理我們易構造出關于a,b的方程,求出a,b值后易得函數的解析式.
(2)根據(1)的結論,結合二次函數的性質,我們易判斷函數在區間[0,1]上的最值,由于函數是連續函數,故可得函數f(x)的值域.
解答:解:(1)∵f(x)>0的解集是(-3,2),
∴-3,2是方程ax
2+(b-8)x-a-ab=0的兩個根,
∴-3+2=-1=
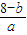
,即b-8=a①
-3×2=-6=
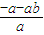
,即1+b=6②
解得a=-3,b=5
∴f(x)=-3x
2-3x+18
(2)∵函數f(x)=-3x
2-3x+18的圖象是以x=
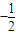
為對稱軸,開口方向朝下的拋物線
故函數f(x)=-3x
2-3x+18在區間[0,1]上單調遞減
∴當x=0時,y有最大值18,
當x=1時,y有最小值12,
∴當x∈[0,1]時函數f(x)的值域[12,18]
點評:本題考查的知識點是函數零點與方程的根及不等式解集的端點之間的關系,函數的值域,其中根據函數零點與方程的根及不等式解集的端點之間的關系,由不等式f(x)>0的解集是(-3,2),構造關于a,b的方程,進而求出函數的解析式是解答本題的關鍵.

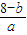 ,即b-8=a①
,即b-8=a①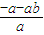 ,即1+b=6②
,即1+b=6②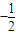 為對稱軸,開口方向朝下的拋物線
為對稱軸,開口方向朝下的拋物線

 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案