
【題目】為提高產品質量,某企業質量管理部門經常不定期地抽查產品進行檢測,現在某條生產線上隨機抽取100個產品進行相關數據的對比,并對每個產品進行綜合評分(滿分100分),將每個產品所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為80分及以上的產品為一等品.
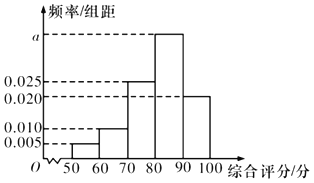
(1)求圖中![]() 的值,并求綜合評分的中位數;
的值,并求綜合評分的中位數;
(2)用樣本估計總體,以頻率作為概率,按分層抽樣的思想,先在該條生產線中隨機抽取5個產品,再從這5個產品中隨機抽取2個產品記錄有關數據,求這2個產品中恰有一個一等品的概率.
【答案】(1) ![]() ;中位數為82.5. (2)
;中位數為82.5. (2) ![]()
【解析】
(1)根據頻率之和為1,結合頻率分布直方圖對應矩形區域面積求解即可;先結合數值預判中位數所在組距應在80到90之間,設綜合評分的中位數為![]() ,結合頻率計算公式求解即可;
,結合頻率計算公式求解即可;
(2)先結合分層抽樣計算出一等品所占比例,再采用列舉法表示出所有基本事件,結合古典概率公式求解即可
(1)由頻率和為1,得![]() ,
,![]() ;
;
設綜合評分的中位數為![]() ,則
,則![]() ,解得
,解得![]() ,
,
所以綜合評分的中位數為82.5.
(2)由頻率分布直方圖知,一等品的頻率為![]() ,即概率為0.6;
,即概率為0.6;
所以100個產品中一等品有60個,非一等品有40個,則一等品與非一等品的抽樣比為3:2;
所以現抽取5個產品,一等品有3個,記為![]() 、
、![]() 、
、![]() ,非一等品2個,記為
,非一等品2個,記為![]() 、
、![]() ;
;
從這5個產品中隨機抽取2個,基本事件為:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共10種;
共10種;
抽取的這2個產品中恰有一個一等品的事件為:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共6種,
共6種,
所以所求的概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為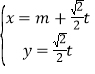 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,橢圓
軸正半軸為極軸建立極坐標系,橢圓![]() 的極坐標方程為
的極坐標方程為![]() ,其左焦點
,其左焦點![]() 在直線
在直線![]() 上.
上.
(1)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求橢圓![]() 的內接矩形面積的最大值.
的內接矩形面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
①![]() 中,
中,![]() 是
是![]() 成立的充要條件;
成立的充要條件;
②當![]() 時,有
時,有![]() ;
;
③已知![]() 是等差數列
是等差數列![]() 的前n項和,若
的前n項和,若![]() ,則
,則![]() ;
;
④若函數![]() 為
為![]() 上的奇函數,則函數
上的奇函數,則函數![]() 的圖象一定關于點
的圖象一定關于點![]() 成中心對稱.其中所有正確命題的序號為___________.
成中心對稱.其中所有正確命題的序號為___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,A、B兩點的坐標分別為(0,1)、(0,﹣1),動點P滿足直線AP與直線BP的斜率之積為![]() ,直線AP、BP與直線y=﹣2分別交于點M、N.
,直線AP、BP與直線y=﹣2分別交于點M、N.
(1)求動點P的軌跡方程;
(2)求線段MN的最小值;
(3)以MN為直徑的圓是否經過某定點?若經過定點,求出定點的坐標;若不經過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銀川市房管局為了了解該市市民2018年1月至2019年1月期間購買二手房情況,首先隨機抽樣其中200名購房者,并對其購房面積m(單位:平方米,![]() )進行了一次調查統計,制成了如圖所示的頻率分布直方圖.
)進行了一次調查統計,制成了如圖所示的頻率分布直方圖.
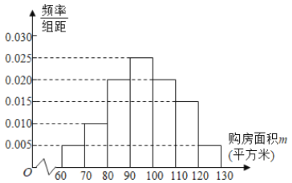
(Ⅰ)試估計該市市民的平均購房面積:
(Ⅱ)現采用分層抽樣的方法從購房面積位于![]() 的40位市民中隨機取4人,再從這4人中隨機抽取2人,求這2人的購房面積恰好有一人在
的40位市民中隨機取4人,再從這4人中隨機抽取2人,求這2人的購房面積恰好有一人在![]() 的概率,
的概率,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數,
為自然對數的底數,![]() .
.
(1)討論函數![]() 的單調性,并寫出相應的單調區間;
的單調性,并寫出相應的單調區間;
(2)已知![]() ,
,![]() ,若
,若![]() 對任意
對任意![]() 都成立,求
都成立,求![]() 的最大值;
的最大值;
(3)設![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的身體狀況,某校隨機抽取了一批學生測量體重.經統計,這批學生的體重數據(單位:千克)全部介于45至70之間.將數據分成以下5組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到如圖所示的頻率分布直方圖,現采用分層抽樣的方法,從第3,4,5組中隨機抽取6名學生,則第3,4,5組抽取的學生人數依次為( )
,得到如圖所示的頻率分布直方圖,現采用分層抽樣的方法,從第3,4,5組中隨機抽取6名學生,則第3,4,5組抽取的學生人數依次為( )
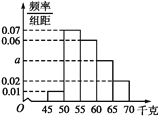
A.4,5,6B.3,2,1C.2,4,5D.2,1,3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某游戲棋盤上標有第![]() 站,棋子開始位于第
站,棋子開始位于第![]() 站,選手拋擲均勻骰子進行游戲,若擲出骰子向上的點數不大于
站,選手拋擲均勻骰子進行游戲,若擲出骰子向上的點數不大于![]() ,棋子向前跳出一站;否則,棋子向前跳出兩站,直到跳到第
,棋子向前跳出一站;否則,棋子向前跳出兩站,直到跳到第![]() 站或第
站或第![]() 站時,游戲結束.設游戲過程中棋子出現在第
站時,游戲結束.設游戲過程中棋子出現在第![]() 站的概率為
站的概率為![]() .
.
(1)當游戲開始時,若拋擲均勻骰子![]() 次后,求棋子所走站數之和
次后,求棋子所走站數之和![]() 的分布列與數學期望;
的分布列與數學期望;
(2)證明:![]() ;
;
(3)若最終棋子落在第![]() 站,則記選手落敗,若最終棋子落在第
站,則記選手落敗,若最終棋子落在第![]() 站,則記選手獲勝.請分析這個游戲是否公平.
站,則記選手獲勝.請分析這個游戲是否公平.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com