
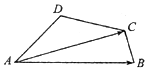
 在四邊形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,則$\overrightarrow{AB}$•$\overrightarrow{AC}$=3.
在四邊形ABCD中,∠ADC=∠BCD=120°,AD=DC=2CB=1,則$\overrightarrow{AB}$•$\overrightarrow{AC}$=3. 分析 依題意,利用余弦定理可求得|AC|=$\sqrt{3}$,繼而可得∠ACB=90°,|AB|cos∠CAB=|AC|,利用平面向量數量積的定義即可求得$\overrightarrow{AB}$•$\overrightarrow{AC}$的值.
解答 解: 在三角形ADC中,∠ADC=120°,AD=DC=1,
在三角形ADC中,∠ADC=120°,AD=DC=1,
由余弦定理得:|AC|2=|AD|2+|CD|2-2|AD||CD|cos120°=1+1-2×(-$\frac{1}{2}$)=3,
故|AC|=$\sqrt{3}$,
又∠DAC=∠DCA=30°,∠BCD=120°,
所以,∠ACB=90°,即△ACB為直角三角形,
所以,|AB|cos∠CAB=|AC|,
所以$\overrightarrow{AB}$•$\overrightarrow{AC}$=|AB||AC|cos∠CAB=|AC|(|AB|cos∠CAB)=|AC|•|AC|=$\sqrt{3}$•$\sqrt{3}$=3.
故答案為:3.
點評 本題考查平面向量數量積的運算,考查余弦定理的應用與平面向量數量積的定義,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
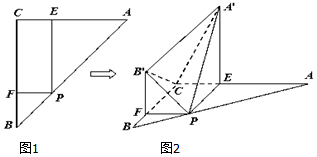 如圖,在△ABC中,∠C=90°,AC=BC=a,點P在邊AB上,設$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),過點P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE將△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF將△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.
如圖,在△ABC中,∠C=90°,AC=BC=a,點P在邊AB上,設$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ>0),過點P作PE∥BC交AC于E,作PF∥AC交BC于F.沿PE將△APE翻折成△A′PE,使平面A′PE⊥平面ABC;沿PF將△BPF翻折成△B′PF,使平面B′PF⊥平面ABC.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
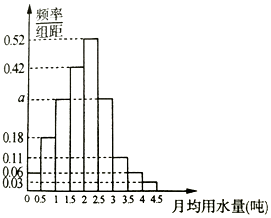 我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準x(噸),一位居民的月用水量不超過x的部分按平價收費,超過x的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5)分成9組,制成了如圖所示的頻率分布直方圖.
我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準x(噸),一位居民的月用水量不超過x的部分按平價收費,超過x的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5)分成9組,制成了如圖所示的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 4 | 6 | 8 | 10 | 12 |
| y | 1 | 2 | 3 | 5 | 6 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com