
【題目】已知圓C過兩點A(0,4),B(4,6),且圓心在直線x﹣2y﹣2=0上.
(1)求圓C的方程;
(2)若直線l過原點且被圓C截得的弦長為6,求直線l的方程.
【答案】(1)(x﹣4)2+(y﹣1)2=25(2)x=0或15x+8y=0
【解析】
(1)線段![]() 的垂直平分線為
的垂直平分線為![]() 與直線
與直線![]() 聯(lián)立,求出圓心坐標(biāo),半徑,即可求圓
聯(lián)立,求出圓心坐標(biāo),半徑,即可求圓![]() 的方程;
的方程;
(2)分類討論,求出圓心![]() 到直線
到直線![]() 的距離,利用直線
的距離,利用直線![]() 過原點且被圓
過原點且被圓![]() 截得的弦長為6,結(jié)合勾股定理,求出
截得的弦長為6,結(jié)合勾股定理,求出![]() ,即可求直線
,即可求直線![]() 的方程.
的方程.
解:(1)線段![]() 的垂直平分線為
的垂直平分線為![]() 與直線
與直線![]() 聯(lián)立
聯(lián)立
可得圓心![]() ,
,
![]() 半徑
半徑![]() ,
,
故所求圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() .
.
(2)當(dāng)直線![]() 的斜率不存在時,
的斜率不存在時,![]() 顯然滿足題意;
顯然滿足題意;
當(dāng)直線![]() 的斜率存在時,設(shè)直線
的斜率存在時,設(shè)直線![]() ,
,
![]() 弦長為6,
弦長為6,![]() 圓心
圓心![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
即![]() ,解得
,解得![]() ,此時直線
,此時直線![]() ,
,
故所求直線![]() 的方程為
的方程為![]() 或
或![]() .
.


 尖子生新課堂課時作業(yè)系列答案
尖子生新課堂課時作業(yè)系列答案 英才計劃同步課時高效訓(xùn)練系列答案
英才計劃同步課時高效訓(xùn)練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】等腰直角三角形![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
于![]() ,如圖①.將
,如圖①.將![]() 沿
沿![]() 折起,使
折起,使![]() 到達(dá)
到達(dá)![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,連接
,連接![]() ,
,![]() ,如圖②.
,如圖②.
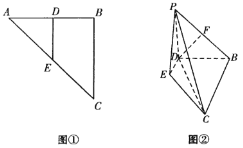
(Ⅰ)若![]() 為
為![]() 的中點,
的中點,![]() ,求證:
,求證:![]() ;
;
(Ⅱ)若![]() ,當(dāng)三棱錐
,當(dāng)三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等差數(shù)列![]() 中,
中,![]() ,
,![]() .令
.令![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)是否存在正整數(shù)![]() ,(
,(![]()
![]() ),使得
),使得![]() ,
,![]() ,
,![]() 成等比數(shù)列?若存在,求出所有的
成等比數(shù)列?若存在,求出所有的![]() ,
,![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】司機在開機動車時使用手機是違法行為,會存在嚴(yán)重的安全隱患,危及自己和他人的生命. 為了研究司機開車時使用手機的情況,交警部門調(diào)查了![]() 名機動車司機,得到以下統(tǒng)計:在
名機動車司機,得到以下統(tǒng)計:在![]() 名男性司機中,開車時使用手機的有
名男性司機中,開車時使用手機的有![]() 人,開車時不使用手機的有
人,開車時不使用手機的有![]() 人;在
人;在![]() 名女性司機中,開車時使用手機的有
名女性司機中,開車時使用手機的有![]() 人,開車時不使用手機的有
人,開車時不使用手機的有![]() 人.
人.
(1)完成下面的![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認(rèn)為開車時使用手機與司機的性別有關(guān);
的把握認(rèn)為開車時使用手機與司機的性別有關(guān);
開車時使用手機 | 開車時不使用手機 | 合計 | |
男性司機人數(shù) | |||
女性司機人數(shù) | |||
合計 |
(2)以上述的樣本數(shù)據(jù)來估計總體,現(xiàn)交警部門從道路上行駛的大量機動車中隨機抽檢3輛,記這3輛車中司機為男性且開車時使用手機的車輛數(shù)為![]() ,若每次抽檢的結(jié)果都相互獨立,求
,若每次抽檢的結(jié)果都相互獨立,求![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
參考公式與數(shù)據(jù):
參考數(shù)據(jù):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式
 span>,其中
span>,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖①,在直角梯形ABCD中,AD=1,AD∥BC,AB⊥BC,BD⊥DC,點E是BC邊的中點,將△ABD沿BD折起,使平面ABD⊥平面BCD,連接AE,AC,DE,得到如圖②所示的幾何體.
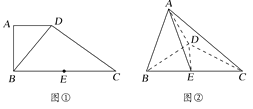
(1)求證:AB⊥平面ADC;
(2)若AC與平面ABD所成角的正切值為![]() ,求二面角B—AD—E的余弦值。
,求二面角B—AD—E的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】河北省高考改革后高中學(xué)生實施選課走班制,若某校學(xué)生選擇物理學(xué)科的人數(shù)為800人,高二期中測試后,由學(xué)生的物理成績,調(diào)研選課走班制學(xué)生的學(xué)習(xí)情況及效果,為此決定從這800人中抽取![]() 人,其頻率分布情況如下:
人,其頻率分布情況如下:
分?jǐn)?shù) | 頻數(shù) | 頻率 |
| 8 | 0.08 |
| 18 | 0.18 |
| 20 | 0.2 |
|
| 0.24 |
| 15 |
|
| 10 | 0.10 |
| 5 | 0.05 |
合計 |
| 1 |
(1)計算表格中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)為了了解成績在![]() ,
,![]() 分?jǐn)?shù)段學(xué)生的情況,先決定利用分層抽樣的方法從這兩個分?jǐn)?shù)段中抽取6人,再從這6人中隨機抽取2人進行面談,求2人來自不同分?jǐn)?shù)段的概率.
分?jǐn)?shù)段學(xué)生的情況,先決定利用分層抽樣的方法從這兩個分?jǐn)?shù)段中抽取6人,再從這6人中隨機抽取2人進行面談,求2人來自不同分?jǐn)?shù)段的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() 分別為橢圓
分別為橢圓![]() :
:![]() 的左右焦點,已知橢圓
的左右焦點,已知橢圓![]() 上的點
上的點![]() 到焦點
到焦點![]() ,
,![]() 的距離之和為4.
的距離之和為4.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作直線交橢圓
作直線交橢圓![]() 于
于![]() ,
,![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,連結(jié)
,連結(jié)![]() 并延長交橢圓于點
并延長交橢圓于點![]() (
(![]() 為坐標(biāo)原點),若
為坐標(biāo)原點),若![]() ,
,![]() ,
,![]() 等比數(shù)列,求線段
等比數(shù)列,求線段![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ;
;![]() .
.
(1)判斷![]() 在
在![]() 上的單調(diào)性,并說明理由;
上的單調(diào)性,并說明理由;
(2)求![]() 的極值;
的極值;
(3)當(dāng)![]() 時,
時,![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com