【題目】設
,
分別為橢圓
:
的左右焦點,已知橢圓上的點
到焦點,的距離之和為4.
(1)求橢圓的方程;
(2)過點作直線交橢圓于
,
兩點,線段
的中點為
,連結
并延長交橢圓于點
(
為坐標原點),若
,
,
等比數列,求線段的方程.
【答案】（1）
.（2）
.
【解析】
（1）根據橢圓定義，代入點
，得到
和
，從而得到橢圓方程；（2）根據（1）得到
，根據題意得到
，當直線
斜率不存在時，說明不成立，當直線斜率存在，設為
，與橢圓聯立得到
，
，再得到
點坐標，求出
方程，得到
，利用弦長公式，得到
，從而得到關于
的方程，解得值，得到的方程.
解:（1）因為橢圓
上的點到焦點
，
的距離之和為4
所以
，即
，
將點代入橢圓方程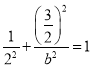得
，得
，
故橢圓方程為.
（2）因為
，
所以焦點的坐標分別為
和
，，
因為
，
，成等比數列，
所以.
①當直線斜率不存在時，則所求方程為
，
，
.
顯然不符合題意.
②當直線斜率存在，并設直線方程為，
代入得
，
設
，
，則
，
，
所以
，
，
即點坐標為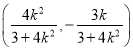
，
所以可得直線方程為:
，
代入橢圓方程解得
，
，
故
，
又因為
，
代入，得
，解得
，
故直線的方程為.
步步高達標卷系列答案科目：高中數學 來源： 題型：
【題目】已知
為直平行六面體.命題
為正方體；命題
的任意體對角線與其不相交的面對角線垂直.則命題
是命題
的（ ）條件 .
A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，其圖像相鄰的兩個對稱中心之間的距離為
，且有一條對稱軸為直線
，則下列判斷正確的是 （ ）
A. 函數
的最小正周期為
B. 函數的圖象關于直線
對稱
C. 函數在區間
上單調遞增
D. 函數的圖像關于點
對稱
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2021年廣東新高考將實行“
”模式，即語文、數學、英語必選，物理、歷史二選一，政治、地理、化學、生物四選二，共選六科參加高考.其中偏理方向是二選一時選物理，偏文方向是二選一時選歷史，對后四科選擇沒有限定.
（1）小明隨機選課，求他選擇偏理方向及生物學科的概率；
（2）小明、小吳同時隨機選課，約定選擇偏理方向及生物學科，求他們選課相同的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，曲線C的參數方程為
，（θ為參數），以原點為極點，x軸非負半軸為極軸建立極坐標系．
（1）求曲線C的極坐標方程；
（2）在平面直角坐標系xOy中，A（﹣2，0），B（0，﹣2），M是曲線C上任意一點，求△ABM面積的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
，直線
不過原點
且不平行于坐標軸，與
有兩個交點
，
，線段
的中點為
.證明：
（
）直線
的斜率與的斜率的乘積為定值
.
（
）若過點
，延長線段與交于點
，當四邊形
為平行四邊形時，則直線的斜率
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[2019·朝鮮中學]在如圖所示的程序框圖中，有這樣一個執行框
，其中的函數關系式為
，程序框圖中的
為函數
的定義域．
（1）若輸入
，請寫出輸出的所有
的值；
（2）若輸出的所有
都相等，試求輸入的初始值
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
