
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為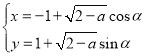 (
(![]() 為參數,
為參數,![]() ).
).
(Ⅰ)當![]() 時,若曲線
時,若曲線![]() 上存在
上存在![]() 兩點關于點
兩點關于點![]() 成中心對稱,求直線
成中心對稱,求直線![]() 的參數方程;
的參數方程;
(Ⅱ)在以原點為極點,![]() 軸正半軸為極軸的極坐標系中,極坐標方程為
軸正半軸為極軸的極坐標系中,極坐標方程為![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若
兩點,若![]() ,求實數
,求實數![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】甲、乙兩企業生產同一種型號零件,按規定該型號零件的質量指標值落在![]() 內為優質品.從兩個企業生產的零件中各隨機抽出了500件,測量這些零件的質量指標值,得結果如下表:
內為優質品.從兩個企業生產的零件中各隨機抽出了500件,測量這些零件的質量指標值,得結果如下表:
甲企業:

乙企業:

(1)已知甲企業的500件零件質量指標值的樣本方差![]() ,該企業生產的零件質量指標值
,該企業生產的零件質量指標值![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為質量指標值的樣本平均數
近似為質量指標值的樣本平均數![]() (注:求
(注:求![]() 時,同一組數據用該區間的中點值作代表),
時,同一組數據用該區間的中點值作代表),![]() 近似為樣本方差
近似為樣本方差![]() ,試根據該企業的抽樣數據,估計所生產的零件中,質量指標值不低于71.92的產品的概率.(精確到0.001)
,試根據該企業的抽樣數據,估計所生產的零件中,質量指標值不低于71.92的產品的概率.(精確到0.001)
(2)由以上統計數據完成下面![]() 列聯表,并問能否在犯錯誤的概率不超過0.01的前提下,認為“兩個分廠生產的零件的質量有差異”.
列聯表,并問能否在犯錯誤的概率不超過0.01的前提下,認為“兩個分廠生產的零件的質量有差異”.

附注:
參考數據: ![]() ,
,
參考公式: ![]() ,
, ![]() ,
,
![]() .
.
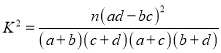
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
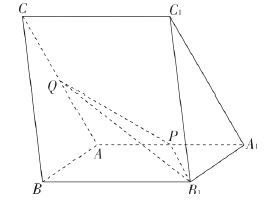
【題目】如圖,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分別為棱
分別為棱![]() 的中點.
的中點.
(1)在平面![]() 內過點
內過點![]() 作
作![]() 平面
平面![]() 交
交![]() 于點
于點![]() ,并寫出作圖步驟,但不要求證明.
,并寫出作圖步驟,但不要求證明.
(2)若側面![]() 側面
側面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子公司開發一種智能手機的配件,每個配件的成本是15元,銷售價是20元,月平均銷售![]() 件,通過改進工藝,每個配件的成本不變,質量和技術含金量提高,市場分析的結果表明,如果每個配件的銷售價提高的百分率為
件,通過改進工藝,每個配件的成本不變,質量和技術含金量提高,市場分析的結果表明,如果每個配件的銷售價提高的百分率為![]() ,那么月平均銷售量減少的百分率為
,那么月平均銷售量減少的百分率為![]() ,記改進工藝后電子公司銷售該配件的月平均利潤是
,記改進工藝后電子公司銷售該配件的月平均利潤是![]() (元).
(元).
(1)寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)改進工藝后,試確定該智能手機配件的售價,使電子公司銷售該配件的月平均利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x2﹣kx﹣4在區間[﹣2,4]上具有單調性,則k的取值范圍是( )
A.[﹣8,16]
B.(﹣∞,﹣8]∪[16,+∞)
C.(﹣∞,﹣8)∪(16,+∞)
D.[16,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列每組函數是同一函數的是( )
A.f(x)=x0與f(x)=1
B.f(x)= ![]() ﹣1與f(x)=|x|﹣1
﹣1與f(x)=|x|﹣1
C.f(x)= ![]() 與f(x)=x﹣2
與f(x)=x﹣2
D.f(x)= ![]() 與f(x)=
與f(x)= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:
滿足:![]() 恒等于常數
恒等于常數![]() ,則稱
,則稱![]() 具有局部等差數列
具有局部等差數列![]() .
.
(1)若![]() 具有局部等差數列
具有局部等差數列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若無窮數列![]() 是等差數列,無窮數列
是等差數列,無窮數列![]() 是公比為正數的等比數列,
是公比為正數的等比數列,![]() ,
,![]() ,
,![]() ,判斷
,判斷![]() 是否具有局部等差數列
是否具有局部等差數列![]() ,并說明理由;
,并說明理由;
(3)設![]() 既具有局部等差數列
既具有局部等差數列![]() ,又具有局部等差數列
,又具有局部等差數列![]() ,求證:
,求證:![]() 具有局部等差數列
具有局部等差數列![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com