【題目】已知函數
．
（Ⅰ）當
時，討論函數
的單調性；
（Ⅱ）當
，且
時，求證：
．
【答案】見解析
【解析】（Ⅰ）
．………………1分
當
時，
，則
時，
，
單調遞增；
時， 
，單調遞減．………………2分
當
時，令
，得
或
．
①當
時，
，則當
時，
，
單調遞減；當
時，
，單調遞增；當
時，，單調遞減；
②當
時，
，
恒成立，
在
上單調遞減，無增區間；………………4分
綜上，當時，
的單調減區間是
，單調增區間是
；當時，的單調減區間是
，單調增區間是
；當時，的單調減區間是，無增區間．………………5分
（Ⅱ）由（Ⅰ）知
，則為了證明：
，
只需證明
，
即證：
．………………6分
令
，則
．………………7分
令
，則
．………………8分
因為
，且
，所以
，
，
所以
，………………9分
所以
在
上單調遞增，則
，即
，
所以函數
在上單調遞增，
，………………10分
即不等式
成立，
故不等式成立．………………12分
【命題意圖】本題主要考查利用導數研究函數的單調性、導數在不等式中的應用，意在考查學生的邏輯推理能力、運算求解能力以及分類討論思想．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】如圖,在直角梯形ABCD中AD∥BC,∠ADC＝90°,平面ABCD外一點P在平面ABCD內的射影Q恰在邊AD上, PA＝AD＝2 BC＝2,CD＝.
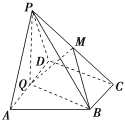
(1)若平面PQB⊥平面PAD,求證：Q為線段AD中點；
(2)在(1)的條件下,若M在線段PC上,且PA∥平面BMQ,求點M到平面PAB的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個質地均勻的正四面體的四個面上分別標示著數字1，2，3，4，一個質地均勻的骰子（正方體）的六個面上分別標示數字1，2，3，4，5，6，先后拋擲一次正四面體和骰子.
（1）列舉出全部基本事件；
（2）求被壓在底部的兩個數字之和小于5的概率；
（3）求正四面體上被壓住的數字不小于骰子上被壓住的數字的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系中，已知曲線
的參數方程為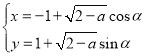
（
為參數，
）．
（Ⅰ）當
時，若曲線上存在
兩點關于點
成中心對稱，求直線
的參數方程；
（Ⅱ）在以原點為極點，
軸正半軸為極軸的極坐標系中，極坐標方程為
的直線
與曲線相交于
兩點，若
，求實數
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
（a＞0，a≠1）．
（1）判斷函數f（x）的奇偶性；
（2）判斷函數f（x）在（1，+∞）上的單調性，并給出證明；
（3）當x∈（n，a﹣2）時，函數f（x）的值域是（1，+∞），求實數a與n的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的左焦點為
，設
是橢圓
的兩個短軸端點，
是橢圓
的長軸左端點．
（Ⅰ）當
時，設點
，直線
交橢圓
于
，且直線
的斜率分別為
，求
的值；
（Ⅱ）當
時，若經過
的直線
與橢圓
交于
兩點，O為坐標原點，求
與
的面積之差的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學為了解2017屆高三學生的性別和喜愛游泳是否有關，對100名高三學生進行了問卷調查，得到如下列聯表：
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 |
已知在這100人中隨機抽取1人，抽到喜歡游泳的學生的概率為
．
（Ⅰ）請將上述列聯表補充完整；
（Ⅱ）判斷是否有99.9%的把握認為喜歡游泳與性別有關？
附： 
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
