
設f(x)是(-∞,+∞)上的奇函數,f(x+2)=-f(x),當0≤x≤1時,f(x)=x.
(1)求f(π)的值;
(2)當-4≤x≤4時,求f(x)的圖象與x軸所圍成圖形的面積;
(3)寫出(-∞,+∞)內函數f(x)的單調區間.
(1)π-4.
(2)4
(3)遞增區間為[4k-1,4k+1](k∈Z),單調遞減區間[4k+1,4k+3](k∈Z)
【解析】
試題分析:解:(1)由f(x+2)=-f(x)得,
f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),
所以f(x)是以4為周期的周期函數,
∴f(π)=f(-1×4+π)=f(π-4)=-f(4-π)=-(4-π)=π-4.
(2)由f(x)是奇函數與f(x+2)=-f(x),得:f[(x-1)+2]=-f(x-1)=f[-(x-1)],即f(1+x)=f(1-x).
故知函數y=f(x)的圖象關于直線x=1對稱.
又0≤x≤1時,f(x)=x,且f(x)的圖象關于原點成中心對稱,則f(x)的圖象如圖所示.
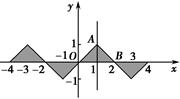
當-4≤x≤4時,f(x)的圖象與x軸圍成的圖形面積為S,則
S=4S△OAB=4×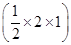 =4.
=4.
(3)根據(1)(2)可知函數的圖形,根據奇偶性以及解析式和對稱中心可知,
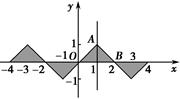
在一個周期[-1,3]內的圖象可知增區間為[-1,1],減區間為[1,3],那么推廣到整個實數域可知,都加上周期的整數倍即可,故可知函數f(x)的單調遞增區間為[4k-1,4k+1](k∈Z),單調遞減區間[4k+1,4k+3](k∈Z)
考點:函數圖象與性質
點評:主要是考查了函數的圖象與性質的綜合運用,屬于中檔題。


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
(1)試證:x=1是函數f(x)的一條對稱軸;
(2)證明函數f(x)是以4為周期的函數,并求x∈[1,5]時,f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
A.a<-1或a>![]() B.-l<a<
B.-l<a<![]()
C.a<![]() D.a<
D.a<![]() 且a≠-1
且a≠-1
查看答案和解析>>
科目:高中數學 來源:2013-2014學年人教版高考數學文科二輪專題復習提分訓練7練習卷(解析版) 題型:填空題
設f(x)是以2為周期的函數,且當x∈[1,3)時,f(x)=x-2,則f(-1)= .
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河北省高三上學期期末考試文科數學 題型:選擇題
設f(x)是定義在R上的奇函數,且f(2)=0,當x>0時,有 恒成立,則不等式
恒成立,則不等式 的解集是
的解集是
A.(-2,0) ∪(2,+∞) B.(-2,0) ∪(0,2) C.(-∞,-2)∪(2,+∞) D.(-∞,-2)∪(0,2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com