【題目】10名象棋選手進行單循環賽（即每兩名選手比賽一場）．規定兩人對局勝者得2分，平局各得1分，負者得0分，并按總得分由高到低進行排序．比賽結束后，10名選手的得分各不相同，且第二名的得分是最后五名選手得分之和的
．則第二名選手的得分是____．
中考解讀考點精練系列答案
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案科目：高中數學 來源： 題型：
【題目】某校象棋社團組織中國象棋比賽,采用單循環賽制,即要求每個參賽選手必須且只須和其他選手各比賽一場,勝者得
分,負者得
分,平局兩人各得
分.若冠軍獲得者得分比其他人都多,且獲勝場次比其他人都少,則本次比賽的參賽人數至少為
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，直線l的參數方程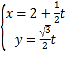
(t為參數)，以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C的極坐標方程為：
．
Ⅰ
直線l的參數方程化為極坐標方程；
Ⅱ求直線l與曲線C交點的極坐標其中
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數f（x），若f（x0）＝x0，則稱x0為f（x）的不動點.設f（x）＝x3+ax2+bx+3.
（1）當a＝0時，
（i）求f（x）的極值點；
（ⅱ）若存在x0既是f（x）的極值點，也是f（x）的不動點，求b的值；
（2）是否存在a，b，使得f（x）有兩個極值點，且這兩個極值點均為f（x）的不動點？說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，
分別在
軸，
軸上運動，
，點
在線段
上，且
.
（1）求點的軌跡
的方程；
（2）直線
與交于
，
兩點，
，若直線
，
的斜率之和為2，直線是否恒過定點？若是，求出定點的坐標；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某校舉行的航天知識競賽中，參與競賽的文科生與理科生人數之比為
，且成績分布在
，分數在
以上（含）的同學獲獎. 按文理科用分層抽樣的方法抽取
人的成績作為樣本，得到成績的頻率分布直方圖（見下圖）.
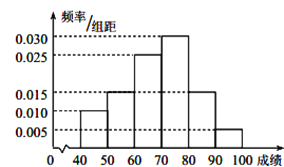
（I）在答題卡上填寫下面的
列聯表，能否有超過
的把握認為“獲獎與學生的文理科有關”？
文科生 | 理科生 | 合計 | |
獲獎 |
| ||
不獲獎 | |||
合計 |
|
（II）將上述調査所得的頻率視為概率，現從該校參與競賽的學生中，任意抽取
名學生，記“獲獎”學生人數為
，求的分布列及數學期望.
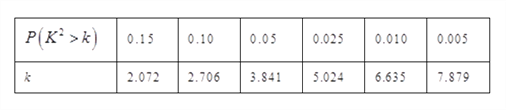
附表及公式：
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
