分析:作出函數f(x)的圖象,得到圖象是由圓心角為直角的扇形AOB和線段BC構成,從而得到f(x)的圖象繞x軸旋轉一周,所得幾何體是由半球和圓錐組合而成的幾何體.由此結合題中的數據加以計算,可得本題答案.
解答:解:根據題意,作出圖象,可得
函數
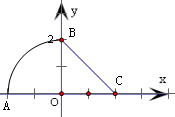
f(x)=的圖象是由圓心角為直角的扇形AOB
和線段BC構成,其中A(-2,0),B(0,2),C(2,0)
因此,該圖象繞x軸旋轉一周,所得幾何體是由半球和圓錐組合而成
半球的半徑R=2,圓錐的底面半徑為2,高等于2且母線長等于2
∵S
半球=
×4π×2
2=8π,S
圓錐側=
π×2×2=
4π∴所得幾何體的表面積為S=S
半球+S
圓錐側=
(8+4)π又∵V
半球=
×
×23=
,V
圓錐=
×π×2
2×2=
∴所得幾何體的體積為V=V
半球+V
圓錐=
+
=8π
故答案為:
(8+4)π;8π 點評:本題將分段函數的圖象繞x軸旋轉一周,求旋轉成的幾何體的表面積和體積.著重考查了球和圓錐的表面積公式、體積公式和函數圖象的作法等知識,屬于中檔題.



