
在△ABC中,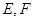 分別是
分別是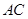 ,
, 的中點,且
的中點,且 ,若
,若 恒成立,則
恒成立,則 的最小值為( )
的最小值為( )
A.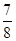 | B. | C. | D.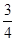 |
A
解析試題分析:如圖所示: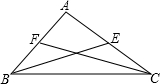
∵3AB=2AC,∴AC=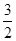 AB,
AB,
又E、F分別為AC、AB的中點,
∴AE=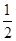 AC,AF=
AC,AF=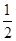 AB,
AB,
∴在△ABE中,由余弦定理得:BE2=AB2+AE2-2AB•AE•cosA
=AB2+(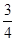 AB)2-2AB•
AB)2-2AB•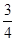 AB•cosA=
AB•cosA=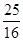 AB2-
AB2-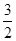 AB2cosA,
AB2cosA,
在△ACF中,由余弦定理得:CF2=AF2+AC2-2AF•AC•cosA
=(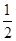 AB)2+(
AB)2+(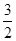 AB)2-2•
AB)2-2•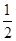 AB•
AB•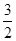 AB•cosA=
AB•cosA=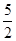 AB2-
AB2-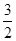 AB2cosA,
AB2cosA,
∴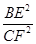 =
=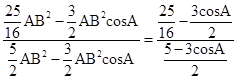 ,
,
∴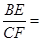
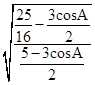 =
=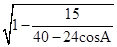 .
.
∵當cosA取最小值時,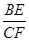 最大,
最大,
∴當A→π時,cosA→-1,此時 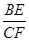 達到最大值,最大值為
達到最大值,最大值為  ,
,
故  恒成立,t的最小值為
恒成立,t的最小值為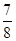 .選A.
.選A.
考點:余弦定理,余弦函數的性質,不等式恒成立問題。
點評:中檔題,不等式恒成立問題,往往通過“分離參數”,轉化成求函數的最值問題,解答本題的關鍵是,熟練掌握余弦定理,利用余弦定理建立三角形的邊角關系。


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com