
設函數 的定義域為R,若存在常數M>0,使
的定義域為R,若存在常數M>0,使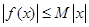 對 一切實數x均成 立,則稱
對 一切實數x均成 立,則稱 為“倍約束函數”,現給出下列函數:①
為“倍約束函數”,現給出下列函數:① :②
:②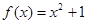 :③
:③ ;④
;④ ⑤
⑤ 是定義在實數集R上的奇函數,且
是定義在實數集R上的奇函數,且
對一切 均有
均有 ,其中是“倍約束函數”的有( )
,其中是“倍約束函數”的有( )
| A.1個 | B.2個 | C.3個 | D.4個 |
C
解析試題分析:解:①對于函數 ,存在
,存在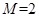 ,使
,使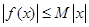 對 一切實數x均成 立,所以該函數是“倍約束函數”;
對 一切實數x均成 立,所以該函數是“倍約束函數”;
②對于函數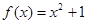 ,當
,當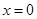 時,
時, ,故不存在常數M>0,使
,故不存在常數M>0,使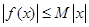 對 一切實數x均成 立,所以該函數不是“倍約束函數”;
對 一切實數x均成 立,所以該函數不是“倍約束函數”;
③對于函數 ,當
,當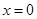 時,
時, ,故不存在常數M>0,使
,故不存在常數M>0,使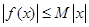 對 一切實數x均成 立,所以該函數不是“倍約束函數”;
對 一切實數x均成 立,所以該函數不是“倍約束函數”;
④對于函數 ,因為當
,因為當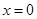 時,
時, ;
;
當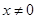 時,
時,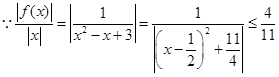 ,所以存在常數
,所以存在常數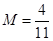 ,使
,使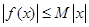 對 一切實數x均成 立, 所以該函數是“倍約束函數”;
對 一切實數x均成 立, 所以該函數是“倍約束函數”;
⑤由題設 是定義在實數集R上的奇函數,
是定義在實數集R上的奇函數,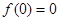 ,所以在
,所以在 中令
中令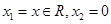 ,于是有
,于是有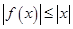 ,即存在常數
,即存在常數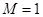 ,使
,使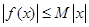 對 一切實數x均成 立, 所以該函數是“倍約束函數”;
對 一切實數x均成 立, 所以該函數是“倍約束函數”;
綜上可知“倍約束函數”的有①④⑤共三個,所以應選C.
考點:1、新定義;2、賦值法;3、基本初等函數的性質.


 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:高中數學 來源: 題型:單選題
函數f(x)的定義域為R,f(-1)=2,對任意x∈R,f′(x)>2,則f(x)>2x+4的解集為( )
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
對實數a與b,定義新運算“?”: .設函數f(x)=(x2﹣2)?(x﹣x2),x∈R.若函數y=f(x)﹣c的圖象與x軸恰有兩個公共點,則實數c的取值范圍是( )
.設函數f(x)=(x2﹣2)?(x﹣x2),x∈R.若函數y=f(x)﹣c的圖象與x軸恰有兩個公共點,則實數c的取值范圍是( )
A.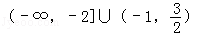 |
B.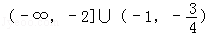 |
C. |
D.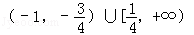 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
己知集合M={﹣1,1,2,4}N={0,1,2}給出下列四個對應法則,其中能構成從M到N的函數是( )
| A.y=x2 | B.y=x+1 | C.y=2x | D.y=log2|x| |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
若 ,則函數
,則函數 的兩個零點分別位于區間( )
的兩個零點分別位于區間( )
| A.(a,b)和(b,c)內 |
| B.(-∞,a)和(a,b)內 |
| C.(b,c)和(c,+∞)內 |
| D.(-∞,a)和(c,+∞)內 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com