
【題目】已知命題![]() :函數
:函數![]() 在
在![]() 上單調遞增;命題
上單調遞增;命題![]() :函數
:函數![]() 在
在![]() 上單調遞減.
上單調遞減.
(Ⅰ)若![]() 是真命題,求實數
是真命題,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() 或
或![]() 為真命題,
為真命題,![]() 且
且![]() 為假命題,求實數
為假命題,求實數![]() 的取值范圍.
的取值范圍.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】羅馬數字是歐洲在阿拉伯數字傳入之前使用的一種數碼,它的產生標志著一種古代文明的進步.羅馬數字的表示法如下:
數字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
形式 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | Ⅸ |
其中“Ⅰ”需要1根火柴,“Ⅴ”與“X”需要2根火柴,若為0,則用空位表示. (如123表示為![]() ,405表示為
,405表示為![]() )如果把6根火柴以適當的方式全部放入下面的表格中,那么可以表示的不同的三位數的個數為( )
)如果把6根火柴以適當的方式全部放入下面的表格中,那么可以表示的不同的三位數的個數為( )
![]()
A.87B.95C.100D.103
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 的焦點,若點
的焦點,若點![]() 在拋物線
在拋物線![]() 上,且
上,且![]()
![]() 求拋物線
求拋物線![]() 的方程;
的方程;
![]() 動直線
動直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 兩點,問:在
兩點,問:在![]() 軸上是否存在定點
軸上是否存在定點![]() 其中
其中![]() ,使得向量
,使得向量![]() 與向量
與向量![]() 共線
共線![]() 其中
其中![]() 為坐標原點
為坐標原點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .現以極點
.現以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸的非負半軸建立平面直角坐標系,直線
軸的非負半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為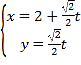 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標系方程和直線
的直角坐標系方程和直線![]() 的普通方程;
的普通方程;
(2)點![]() 在曲線
在曲線![]() 上,且到直線
上,且到直線![]() 的距離為
的距離為![]() ,求符合條件的
,求符合條件的![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知等腰直角三角形![]() 的斜邊
的斜邊![]() 所在直線方程為
所在直線方程為![]() ,其中
,其中![]() 點在
點在![]() 點上方,直角頂點
點上方,直角頂點![]() 的坐標為
的坐標為![]() .
.

(1)求![]() 邊上的高線
邊上的高線![]() 所在直線的方程;
所在直線的方程;
(2)求等腰直角三角形![]() 的外接圓的標準方程;
的外接圓的標準方程;
(3)分別求兩直角邊![]() ,
,![]() 所在直線的方程.
所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某住宅小區為了使居民有一個優雅、舒適的生活環境,計劃建一個八邊形的休閑小區,其主體造型的平面圖是由兩個相同的矩形ABCD和矩形EFGH構成的面積是200 m2的十字形區域,現計劃在正方形MNPQ上建一花壇,造價為4 200元/m2,在四個相同的矩形上(圖中陰影部分)鋪花崗巖地坪,造價為210元/m2,再在四個空角上鋪草坪,造價為80元/m2.
(1)設總造價為S元,AD的邊長為x m,試建立S關于x的函數解析式;
(2)計劃至少要投多少萬元才能建造這個休閑小區?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,實軸長為6,漸近線方程為
,實軸長為6,漸近線方程為![]() ,動點
,動點![]() 在雙曲線左支上,點
在雙曲線左支上,點![]() 為圓
為圓![]() 上一點,則
上一點,則![]() 的最小值為
的最小值為
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com