
【題目】某產品的包裝紙可類比如圖所示的平面圖形,其可看作是由正方形![]() 和等腰梯形
和等腰梯形![]() 拼成,已知
拼成,已知![]() ,
,![]() ,在包裝的過程中,沿著
,在包裝的過程中,沿著![]() 將正方形
將正方形![]() 折起,直至
折起,直至![]() ,得到多面體
,得到多面體![]() ,
,![]() 分別為
分別為![]() 中點.
中點.
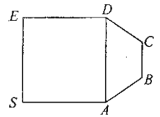
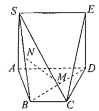
(1)證明:![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積.
的體積.
 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】為豐富學生課外生活,某市組織了高中生鋼筆書法比賽,比賽分兩個階段進行:第一階段由評委給出所有參賽作品評分,并確定優勝者;第二階段為附加賽,參賽人員由組委會按規則另行確定.數據統計員對第一階段的分數進行了統計分析,這些分數![]() 都在
都在![]() 內,在以組距為5畫分數的頻率分布直方圖(設“
內,在以組距為5畫分數的頻率分布直方圖(設“![]() ”)時,發現
”)時,發現![]() 滿足
滿足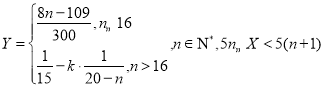 .
.
(1)試確定![]() 的所有取值,并求
的所有取值,并求![]() ;
;
(2)組委會確定:在第一階段比賽中低于85分的參賽者無緣獲獎也不能參加附加賽;分數在![]() 的參賽者評為一等獎;分數在
的參賽者評為一等獎;分數在![]() 的同學評為二等獎,但通過附加賽有
的同學評為二等獎,但通過附加賽有![]() 的概率提升為一等獎;分數在
的概率提升為一等獎;分數在![]() 的同學評為三等獎,但通過附加賽有
的同學評為三等獎,但通過附加賽有![]() 的概率提升為二等獎(所有參加附加賽的獲獎人員均不降低獲獎等級).已知學生
的概率提升為二等獎(所有參加附加賽的獲獎人員均不降低獲獎等級).已知學生![]() 和
和![]() 均參加了本次比賽,且學生
均參加了本次比賽,且學生![]() 在第一階段評為二等獎.
在第一階段評為二等獎.
(![]() )求學生
)求學生![]() 最終獲獎等級不低于學生
最終獲獎等級不低于學生![]() 的最終獲獎等級的概率;
的最終獲獎等級的概率;
(![]() )已知學生
)已知學生![]() 和
和![]() 都獲獎,記
都獲獎,記![]() 兩位同學最終獲得一等獎的人數為
兩位同學最終獲得一等獎的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某傳染病疫情爆發期間,當地政府積極整合醫療資源,建立“艙醫院”對所有密切接觸者進行14天的隔離觀察治療.治療期滿后若檢測指標仍未達到合格標準,則轉入指定專科醫院做進一步的治療.“艙醫院”對所有人員在“入口”及“出口”時都進行了醫學指標檢測,若“入口”檢測指標在35以下者則不需進入“艙醫院”而是直接進入指定專科醫院進行治療.以下是20名進入“艙醫院”的密切接觸者的“入口”及“出口”醫學檢測指標:
入口 | 50 | 35 | 35 | 40 | 55 | 90 | 80 | 60 | 60 | 60 | 65 | 35 | 60 | 90 | 35 | 40 | 55 | 50 | 65 | 50 |
出口 | 70 | 50 | 60 | 50 | 75 | 70 | 85 | 70 | 80 | 70 | 55 | 50 | 75 | 90 | 60 | 60 | 65 | 70 | 75 | 70 |
(Ⅰ)建立![]() 關于
關于![]() 的回歸方程;(回歸方程的系數精確到0.1)
的回歸方程;(回歸方程的系數精確到0.1)
(Ⅱ)如果60是“艙醫院”的“出口”最低合格指標,那么,“入口”指標低于多少時,將來這些密切接觸者將不能進入“艙醫院”而是直接進入指定專科醫院接受治療.(檢測指標為整數)
附注:參考數據:![]() ,
,![]() .
.
參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為: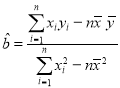 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“搜索指數”是網民通過搜索引擎,以每天搜索關鍵詞的次數為基礎所得到的統計指標.“搜索指數”越大,表示網民對該關鍵詞的搜索次數越多,對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中,某個關鍵詞的搜索指數變化的走勢圖.

根據該走勢圖,下列結論正確的是( )
A. 這半年中,網民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中,網民對該關鍵詞相關的信息關注度不斷減弱
C. 從網民對該關鍵詞的搜索指數來看,去年10月份的方差小于11月份的方差
D. 從網民對該關鍵詞的搜索指數來看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省級示范高中高三年級對各科考試的評價指標中,有“難度系數“和“區分度“兩個指標中,難度系數![]() ,區分度
,區分度![]() .
.
(1)某次數學考試(滿分為150分),隨機從實驗班和普通班各抽取三人,實驗班三人的成績分別為147,142,137;普通班三人的成績分別為97,102,113.通過樣本估計本次考試的區分度(精確0.01).
(2)如表表格是該校高三年級6次數學考試的統計數據:
難度系數x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
區分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①計算相關系數r,|r|<0.75時,認為相關性弱;|r|≥0.75時,認為相關性強.通過計算說明,能否利用線性回歸模型描述y與x的關系(精確到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y關于t的線性回歸方程,并預測x=0.75時y的值(精確到0.01).
附注:參考數據: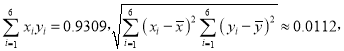
![]()
![]()
參考公式:相關系數 r,回歸直線
r,回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 的焦點
的焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點
的中點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)已知點![]() ,過點
,過點![]() 作直線
作直線![]() 交拋物線于
交拋物線于![]() 、
、![]() 兩點,求
兩點,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值時直線
取得最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國慶節期間,滕州市實驗小學舉行了一次科普知識競賽活動,設置了一等獎、二等獎、三等獎、四等獎及紀念獎,獲獎人數的分配情況如圖所示,各個獎品的單價分別為:一等獎50元、二等獎20元、三等獎10元,四等獎5元,紀念獎2元,則以下說法中不正確的是( )
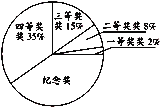
A.獲紀念獎的人數最多B.各個獎項中二等獎的總費用最高
C.購買獎品的費用平均數為6.65元D.購買獎品的費用中位數為5元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,己知
中,己知![]() 是橢圓
是橢圓![]() 的右焦點,
的右焦點,![]() 是橢圓
是橢圓![]() 上位于
上位于![]() 軸上方的任意一點,過
軸上方的任意一點,過![]() 作垂直于
作垂直于![]() 的直線交其右準線
的直線交其右準線![]() 于點
于點![]() .
.
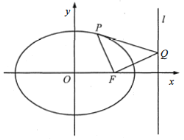
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() ,求證:直線
,求證:直線![]() 與橢圓
與橢圓![]() 相切;
相切;
(3)在橢圓![]() 上是否存在點
上是否存在點![]() ,使四邊形
,使四邊形![]() 是平行四邊形?若存在,求出所有符合條件的點
是平行四邊形?若存在,求出所有符合條件的點![]() 的坐標:若不存在,請說明理由.
的坐標:若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com