(理)(1)證明不等式:ln(1+x)<
(x>0).
(2)已知函數f(x)=ln(1+x)-
在(0,+∞)上單調遞增,求實數a的取值范圍.
(3)若關于x的不等式
+≥1在[0,+∞)上恒成立,求實數b的最大值.
(1)證明:(1)令h(x)=ln(1+x)-
,則h′(x)=
<0∴h(x)在(0,+∞)上單調遞減,即h(x)<h(0)=0
∴ln(1+x)-
<0
∴ln(1+x)<
(x>0).
(2)求導函數,可得f′(x)=
,令f′(x)=0,可得x=0或x=a
2-2a,
∵函數f(x)=ln(1+x)-
在(0,+∞)上單調遞增
∴f′(x)≥0在(0,+∞)上恒成立
∴a
2-2a≤0
∵f(x)在(0,+∞)上有意義
∴a≥0
∴0≤a≤2;
(3)關于x的不等式
+≥1在[0,+∞)上恒成立,等價于
≥1-在[0,+∞)上恒成立,
∵
1-≥0,∴b≥0
當x>0時,b≤1+
-
構造函數g(x)=1+
-
,則
g′(x)=-+由(1)知,ln(1+x)<
(x>0).
以e
x代1+x,可得
x<,
∵x>0,∴-
+>0,
∴g′(x)>0,
∴g(x)在(0,+∞)上單調增
當x>0且x→0時,g(x)→1
∴b≤1
∴實數b的最大值為1
練習冊系列答案
相關習題
科目:高中數學
來源:
題型:
(2012•黃州區模擬)(理)(1)證明不等式:ln(1+x)<
(x>0).
(2)已知函數f(x)=ln(1+x)-
在(0,+∞)上單調遞增,求實數a的取值范圍.
(3)若關于x的不等式
+≥1在[0,+∞)上恒成立,求實數b的最大值.
查看答案和解析>>
科目:高中數學
來源:2012-2013學年山東省青島一中高三(上)1月調研數學試卷(理科)(解析版)
題型:解答題
(理)(1)證明不等式:ln(1+x)<
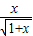
(x>0).
(2)已知函數f(x)=ln(1+x)-
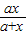
在(0,+∞)上單調遞增,求實數a的取值范圍.
(3)若關于x的不等式
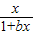
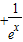
≥1在[0,+∞)上恒成立,求實數b的最大值.
查看答案和解析>>
科目:高中數學
來源:2012-2013學年湖北省武漢市部分學校高三(上)12月月考數學試卷(理科)(解析版)
題型:解答題
(理)(1)證明不等式:ln(1+x)<
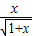
(x>0).
(2)已知函數f(x)=ln(1+x)-

在(0,+∞)上單調遞增,求實數a的取值范圍.
(3)若關于x的不等式
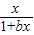
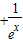
≥1在[0,+∞)上恒成立,求實數b的最大值.
查看答案和解析>>
科目:高中數學
來源:2011-2012學年湖北省黃岡中學等八校高三第二次聯考數學試卷(理科)(解析版)
題型:解答題
(理)(1)證明不等式:ln(1+x)<
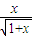
(x>0).
(2)已知函數f(x)=ln(1+x)-
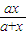
在(0,+∞)上單調遞增,求實數a的取值范圍.
(3)若關于x的不等式
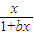
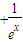
≥1在[0,+∞)上恒成立,求實數b的最大值.
查看答案和解析>>



 閱讀快車系列答案
閱讀快車系列答案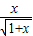 (x>0).
(x>0).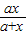 在(0,+∞)上單調遞增,求實數a的取值范圍.
在(0,+∞)上單調遞增,求實數a的取值范圍.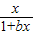
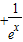 ≥1在[0,+∞)上恒成立,求實數b的最大值.
≥1在[0,+∞)上恒成立,求實數b的最大值.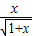 (x>0).
(x>0). 在(0,+∞)上單調遞增,求實數a的取值范圍.
在(0,+∞)上單調遞增,求實數a的取值范圍.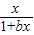
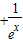 ≥1在[0,+∞)上恒成立,求實數b的最大值.
≥1在[0,+∞)上恒成立,求實數b的最大值.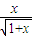 (x>0).
(x>0).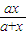 在(0,+∞)上單調遞增,求實數a的取值范圍.
在(0,+∞)上單調遞增,求實數a的取值范圍.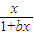
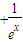 ≥1在[0,+∞)上恒成立,求實數b的最大值.
≥1在[0,+∞)上恒成立,求實數b的最大值.