
【題目】定義域為![]() 的函數
的函數![]() 滿足:對于任意的實數
滿足:對于任意的實數![]() 都有
都有![]() 成立,且當
成立,且當![]() 時,
時, ![]() 恒成立,且
恒成立,且![]() 是一個給定的正整數).
是一個給定的正整數).
(1)判斷函數![]() 的奇偶性,并證明你的結論;
的奇偶性,并證明你的結論;
(2)判斷并證明![]() 的單調性;若函數
的單調性;若函數![]() 在
在![]() 上總有
上總有![]() 成立,試確定
成立,試確定![]() 應滿足的條件;
應滿足的條件;
(3)當![]() 時,解關于
時,解關于![]() 的不等式
的不等式![]() .
.
【答案】(1)![]() 為奇函數,證明見解析;(2)f(x)在(-∞,+∞)上是減函數,證明見解析;f(1)∈[-5,0)(3)①當
為奇函數,證明見解析;(2)f(x)在(-∞,+∞)上是減函數,證明見解析;f(1)∈[-5,0)(3)①當![]() 時,原不等式的解集為
時,原不等式的解集為![]() 或
或![]() ;②當
;②當![]() 時,原不等式的解集為
時,原不等式的解集為![]() ;③當
;③當![]() 時,原不等式的解集為
時,原不等式的解集為![]() 或
或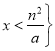 }.
}.
【解析】
(1)利用函數奇偶性的定義,結合抽象函數關系,利用賦值法進行證明;
(2)結合函數單調性的定義以及最值函數成立問題進行證明即可;
(3)利用抽象函數關系,結合函數奇偶性和單調性定義轉化為一元二次不等式,討論參數的范圍進行求解即可;
(1)f(x)為奇函數,證明如下;
由已知對于任意實數x,y都有f(x+y)=f(x)+f(y)恒成立.
令x=y=0,得f(0+0)=f(0)+f(0),所以f(0)=0.
令y=-x,得f(x-x)=f(x)+f(-x)=0.
所以對于任意x,都有f(-x)=-f(x).
所以f(x)是奇函數.
(2)設任意x1,x2且x1<x2,則x2﹣x1>0,由已知f(x2﹣x1)<0,
又f(x2﹣x1)=f(x2)+f(﹣x1)=f(x2)﹣f(x1)<0
得f(x2)<f(x1),
根據函數單調性的定義知f(x)在(﹣∞,+∞) 上是減函數.
所以f(x)在[﹣2,5]上的最大值為f(﹣2).
要使f(x)≤10恒成立,當且僅當f(﹣2)≤10,
又因為f(﹣2)=﹣f(2)=﹣f(1+1)=﹣2f(1)
所以f(1)≥﹣5.
又x>1,f(x)<0,
所以f(1)∈[﹣5,0).
(3)∵![]() .,
.,
∴f(ax2)-f(a2x)>n2[f(x)-f(a)].
所以f(ax2-a2x)>n2f(x-a),
所以f(ax2-a2x)>f[n2(x-a)],
因為f(x)在(-∞,+∞)上是減函數,
所以ax2-a2x<n2(x-a).
即(x-a)(ax-n2)<0,
因為a<0,所以(x-a)(x![]() )>0.
)>0.
討論:
①當a<![]() <0,即a<-n時,原不等式的解集為{x|x>
<0,即a<-n時,原不等式的解集為{x|x>![]() 或x<a};
或x<a};
②當a=![]() ,即a=-n時,原不等式的解集為{x|x≠-n};
,即a=-n時,原不等式的解集為{x|x≠-n};
③當![]() <a<0,即-n<a<0時,原不等式的解集為{x|x>a或x<
<a<0,即-n<a<0時,原不等式的解集為{x|x>a或x<![]() }.
}.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】(2017·全國卷Ⅲ文,18)某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間[20,25),需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高氣溫 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率.
(1)估計六月份這種酸奶一天的需求量不超過300瓶的概率;
(2)設六月份一天銷售這種酸奶的利潤為Y(單位:元).當六月份這種酸奶一天的進貨量為450瓶時,寫出Y的所有可能值,并估計Y大于零的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg)其頻率分布直方圖如下:

(1) 記![]() 表示事件“舊養殖法的箱產量低于50kg”,估計
表示事件“舊養殖法的箱產量低于50kg”,估計![]() 的概率;
的概率;
(2)填寫下面聯表,并根據列聯表判斷是否有![]() %的把握認為箱產量與養殖方法有關:
%的把握認為箱產量與養殖方法有關:
箱產量 | 箱產量 | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,對兩種養殖方法的優劣進行比較.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果函數![]() 的定義域為
的定義域為![]() ,且存在實常數
,且存在實常數![]() ,使得對于定義域內任意
,使得對于定義域內任意![]() ,都有
,都有![]() 成立,則稱此函數
成立,則稱此函數![]() 具有“性質
具有“性質![]() ”.
”.
(1)判斷函數![]() 是否具有“
是否具有“![]() 性質”,若具有“
性質”,若具有“![]() 性質”,求出所有
性質”,求出所有![]() 的值的集合,若不具有“
的值的集合,若不具有“![]() 性質”,請說明理由;
性質”,請說明理由;
(2)已知函數![]() 具有“
具有“![]() 性質”,且當
性質”,且當![]() 時,
時,![]() ,求函數
,求函數![]() 在區間
在區間![]() 上的值域;
上的值域;
(3)已知函數![]() 既具有“
既具有“![]() 性質”,又具有“
性質”,又具有“![]() 性質”,且當
性質”,且當![]() 時,
時,![]() ,若函數
,若函數![]() 的圖像與直線
的圖像與直線![]() 有2017個公共點,求實數
有2017個公共點,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量a=(cos2ωx-sin2ωx,sinωx),b=(![]() ,2cosωx),設函數f(x)=a·b(x∈R)的圖象關于直線x=
,2cosωx),設函數f(x)=a·b(x∈R)的圖象關于直線x=![]() 對稱,其中ω為常數,且ω∈(0,1).
對稱,其中ω為常數,且ω∈(0,1).
(1)求函數f(x)的最小正周期和單調遞增區間;
(2)若將y=f(x)圖象上各點的橫坐標變為原來的![]() ,再將所得圖象向右平移
,再將所得圖象向右平移![]() 個單位,縱坐標不變,得到y=h(x)的圖象,若關于x的方程h(x)+k=0在
個單位,縱坐標不變,得到y=h(x)的圖象,若關于x的方程h(x)+k=0在![]() 上有且只有一個實數解,求實數k的取值范圍.
上有且只有一個實數解,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,E,F分別是C1D1,CC1的中點,則異面直線AE與BF所成角的余弦值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的參數方程為  (t為參數),在以原點O為極點,x軸正半軸為極軸的極坐標系中,圓C的方程為ρ=6sinθ.
(t為參數),在以原點O為極點,x軸正半軸為極軸的極坐標系中,圓C的方程為ρ=6sinθ.
(Ⅰ)寫出直線l的普通方程和圓C的直角坐標方程;
(Ⅱ)設點P(4,3),直線l與圓C相交于A,B兩點,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com