Question

已知點P（x，y）在圓（x-2）²+y²=1上運動，則代數式的最大值是    ．

Answer 1

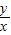
【答案】分析：根據 表示動點（x，y）到定點（0，0）的斜率知：的最大值是圓上的點與原點連線的斜率的最大值，設為k，根據圓心（2，0）到直線kx-y=0的距離等于1，寫出距離公式求出k的最大值．
解答：解∴（x-2）²+y²=1
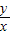
根據 表示動點（x，y）到定點（0，0）的斜率知：
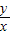
的最大值是圓上的點與原點連線的斜率的最大值，設為k，
∵圓心（2，0）到直線kx-y=0的距離等于1，
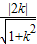
∴=1，
∴，
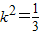
∴k=，
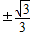
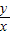
∴代數式的最大值是
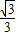
故答案為
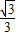點評：本題考查直線與圓的位置關系，本題解題的關鍵是利用數形結合的思想來解出斜率的值，本題是一個中檔題目．