
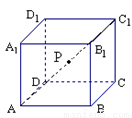
如圖,在棱長為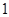 的正方體
的正方體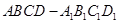 中,
中,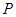 為線段
為線段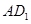 上的點,且滿足
上的點,且滿足
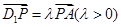 .
.
(Ⅰ)當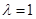 時,求證:平面
時,求證:平面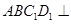 平面
平面 ;
;
(Ⅱ)試證無論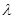 為何值,三棱錐
為何值,三棱錐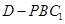 的體積
的體積
恒為定值;
(Ⅲ)求異面直線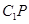 與
與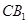 所成的角的余弦值.
所成的角的余弦值.
 18.解:
18.解:
方法一、證明:(Ⅰ)∵正方體 中,
中,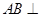 面
面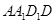 ,
,
又 ∴平面
∴平面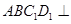 平面
平面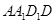 , ………………2分
, ………………2分
∵ 時,
時,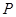 為
為 的中點,∴
的中點,∴ ,
,
又∵平面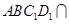 平面
平面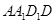
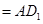 ,
,
∴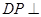 平面
平面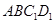 ,
,
又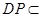 平面
平面 ,∴平面
,∴平面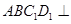 平面
平面 .………4分
.………4分
(Ⅱ)∵ ,
, 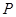 為線段
為線段 上的點,
上的點,
∴三角形 的面積為定值,即
的面積為定值,即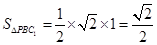 ,
,
………………6分
又∵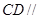 平面
平面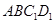 ,∴點
,∴點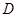 到平面
到平面 的距離為定值,即
的距離為定值,即 , ………………8分
, ………………8分
∴三棱錐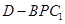 的體積為定值,即
的體積為定值,即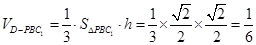 .
.
也即無論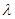 為何值,三棱錐
為何值,三棱錐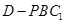 的體積恒為定值
的體積恒為定值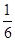 ;………………………10分
;………………………10分
(Ⅲ)∵由(Ⅰ)易知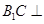 平面
平面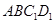 ,
,
又 平面
平面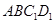 ,∴
,∴ ,
…………………………12分
,
…………………………12分
 即異面直線
即異面直線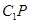 與
與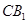 所成的角為定值
所成的角為定值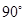 ,從而其余弦值為
,從而其余弦值為 .…………………13分
.…………………13分
方法二、如圖,以點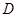 為坐標原點,建立如圖所示的坐標系.
為坐標原點,建立如圖所示的坐標系.
(Ⅰ)當 時,即點
時,即點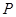 為線段
為線段 的中點,則
的中點,則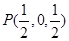 ,又
,又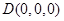 、
、
∴ ,
,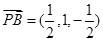 ,設平面
,設平面 的法向量為
的法向量為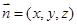 ,……1分
,……1分
則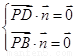 ,即
,即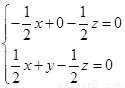 ,令
,令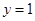 ,解得
,解得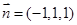 ,
…2分
,
…2分
又∵點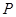 為線段
為線段 的中點,∴
的中點,∴ ,∴
,∴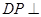 平面
平面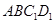 ,
,
∴平面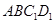 的法向量為
的法向量為 ,
……………3分
,
……………3分
∵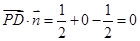 ,
,
∴平面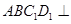 平面
平面 ,
………………………4分
,
………………………4分
(Ⅱ)略;
(Ⅲ)∵ ,∴
,∴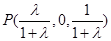 , …………………10分
, …………………10分
又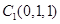 、
、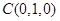 、
、 ,
,
∴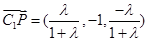 ,
, , ……………………………11分
, ……………………………11分
∵ …………………………………12分
…………………………………12分
∴不管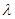 取值多少,都有
取值多少,都有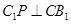 ,即異面直線
,即異面直線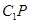 與
與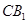 所成的角的余弦值為0.……13分
所成的角的余弦值為0.……13分
【解析】略


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:
 (2013•泉州模擬)如圖,在棱長為1的正方體ABCD-A1B1C1D1的對角線AC1上任取一點P,以A為球心,AP為半徑作一個球.設AP=x,記該球面與正方體表面的交線的長度和為f(x),則函數f(x)的圖象最有可能的是( )
(2013•泉州模擬)如圖,在棱長為1的正方體ABCD-A1B1C1D1的對角線AC1上任取一點P,以A為球心,AP為半徑作一個球.設AP=x,記該球面與正方體表面的交線的長度和為f(x),則函數f(x)的圖象最有可能的是( )查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省泉州市畢業班(第二輪)質量檢測文科數學試卷(解析版) 題型:選擇題
如圖,在棱長為1的正方體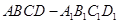 的對角線
的對角線 上任取一點P,以
上任取一點P,以 為球心,
為球心, 為半徑作一個球.設
為半徑作一個球.設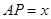 ,記該球面與正方體表面的交線的長度和為
,記該球面與正方體表面的交線的長度和為 ,則函數
,則函數 的圖象最有可能的是( )
的圖象最有可能的是( )

A. B. C. D.
查看答案和解析>>
科目:高中數學 來源:2010年湖北省高三第三次模擬考試(理科)數學卷 題型:選擇題
如圖,在棱長為2的正方體 內有一個內切球O,則過棱
內有一個內切球O,則過棱 和
和 的中點
的中點 、
、 的直線與球面交點為
的直線與球面交點為 、
、 ,則
,則 、
、 兩點間的球面距離為( )
兩點間的球面距離為( )
 A.
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中數學 來源:湖北省黃岡中學2010年高三年級第二次模擬考試(理) 題型:選擇題
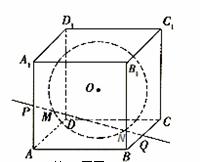 如圖,在棱長為2的正方體
如圖,在棱長為2的正方體 內有一個內切球O,則過棱
內有一個內切球O,則過棱 和
和 的中點
的中點 、
、 的直線與球面交點為
的直線與球面交點為 、
、 ,則
,則 、
、 兩點間的球面距離為 ( )
兩點間的球面距離為 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com