
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,滿足
上的奇函數,滿足![]() ,當
,當![]() 時,有
時,有![]() .
.
(1)求實數![]() 的值;
的值;
(2)求函數![]() 在區間
在區間![]() 上的解析式,并利用定義證明證明其在該區間上的單調性;
上的解析式,并利用定義證明證明其在該區間上的單調性;
(3)解關于![]() 的不等式
的不等式![]() .
.
【答案】(1)![]() ;(2)
;(2) ![]() ;詳見解析(3)
;詳見解析(3)![]()
【解析】
(1)根據![]() 是定義在
是定義在![]() 上的奇函數及
上的奇函數及![]() 時的
時的![]() 解析式即可得出
解析式即可得出![]() ,并可求出
,并可求出![]() ,從而可得出
,從而可得出![]() ,求出
,求出![]() ;(2)根據上面知,
;(2)根據上面知,![]() 時,
時,![]() ,從而可設
,從而可設![]() ,從而得出
,從而得出![]() ,從而得出
,從而得出![]() 時,
時,![]() ,再根據函數單調性的定義即可判斷
,再根據函數單調性的定義即可判斷![]() 在
在![]() 上的單調性.(3)不等式等價于
上的單調性.(3)不等式等價于![]() ,即
,即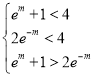 ,解不等式組即得解.
,解不等式組即得解.
(1)![]() 函數
函數![]() 是定義在
是定義在![]() 上的奇函數,
上的奇函數,
![]() ,即
,即![]() ,
,![]() ,
,
又因為![]() (2)
(2)![]() ,所以
,所以![]() (2)
(2)![]() ,
,
即![]() ,所以
,所以![]() ,
,
綜上可知![]() ,
,![]() .經檢驗滿足題意.
.經檢驗滿足題意.
(2)由(1)可知當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,且函數
,且函數![]() 是奇函數,
是奇函數,
![]()
![]() ,
,
![]() 當
當![]() 時,函數
時,函數![]() 的解析式為
的解析式為![]() ,
,
任取![]() ,
,![]() ,且
,且![]() ,則
,則![]() ,
,
![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
于是![]() ,即
,即![]() ,
,
故![]() 在區間
在區間![]() 上是單調增函數;
上是單調增函數;
(3)![]() 是定義在
是定義在![]() 上的奇函數,且
上的奇函數,且![]() ,
,
![]() ,且
,且![]() 在
在![]() 上是增函數,
上是增函數,
![]()
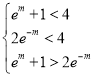 ,解得
,解得![]() ,
,
![]() 原不等式的解集為
原不等式的解集為![]() .
.


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:
【題目】給出下列三個命題,其中所有錯誤命題的序號是______.
![]() 拋物線
拋物線![]() 的準線方程為
的準線方程為![]() ;
;
![]() 過點
過點![]() 作與拋物線
作與拋物線![]() 只有一個公共點的直線t僅有1條;
只有一個公共點的直線t僅有1條;
![]() 是拋物線
是拋物線![]() 上一動點,以P為圓心作與拋物線準線相切的圓,則這個圓一定經過一個定點
上一動點,以P為圓心作與拋物線準線相切的圓,則這個圓一定經過一個定點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某重點中學將全部高一新生分成A,B兩個成績相當(成績的均值、方差都相同)的級部,A級部采用傳統形式的教學方式,B級部采用新型的基于信息化的自主學習教學方式.期末考試后分別從兩個級部中各隨機抽取100名學生的數學成績進行統計,得到如下數據:
A級部教學 成績分組 |
|
|
|
|
|
|
頻數 | 18 | 23 | 29 | 23 | 6 | 1 |
B級部教學 成績分組 |
|
|
|
|
|
|
頻數 | 8 | 16 | 24 | 28 | 21 | 3 |
若成績不低于130分者為“優秀”.
根據上表數據分別估計A,B兩個級部“優秀”的概率;
(2)填寫下面的列聯表,并根據列聯表判斷是否有99%的把握認為“優秀”與教學方式有關?
是否優秀 級部 | 優秀 | 不優秀 | 合計 |
A級部 | |||
B級部 | |||
合計 |
(3)根據上表數據完成下面的頻率分布直方圖,并根據頻率分布直方圖,分別求出A,B兩個級部的中位數的估計值(精確到![]() );請根據以上計算結果初步分析A,B兩個級部的教學成績的優劣.
);請根據以上計算結果初步分析A,B兩個級部的教學成績的優劣.

附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: 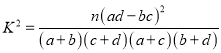
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某旅游景點有50輛自行車供游客租賃使用,管理這些自行車的費用是每日115元。根據經驗,若每輛自行車的日租金不超過6元,則自行車可以全部租出;若超過6元,則每提高1元,租不出去的自行車就增加3輛.規定:每輛自行車的日租金不超過20元,每輛自行車的日租金![]() 元只取整數,并要求出租所有自行車一日的總收入必須超過一日的管理費用,用
元只取整數,并要求出租所有自行車一日的總收入必須超過一日的管理費用,用![]() 表示出租所有自行車的日凈收入(即一日中出租所以自行車的總收入減去管理費用后的所得).
表示出租所有自行車的日凈收入(即一日中出租所以自行車的總收入減去管理費用后的所得).
(1)求函數![]() 的解析式及定義域;
的解析式及定義域;
(2)試問日凈收入最多時每輛自行車的日租金應定為多少元?日凈收入最多為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】央視人民網報道:2019年7月15日,平頂山市文物管理局有關人士表示,郟縣北大街古墓群搶救性發掘工作結束,共發現古墓539座,已發掘墓葬93座。該墓地是一處大型古墓群,在已發掘的93座墓葬中,有戰國時期墓葬32座、兩漢時期墓葬56座、唐墓2座、宋墓3座。生物體死亡后,它機體內原有的碳14會按確定的規律衰減,大約每經過5730年衰減為原來的一半,這個時間稱為“半衰期”.檢測一墓葬女尸出土時碳14的殘余量約占原始含量的79%,則可推斷為該墓葬屬于( )時期(輔助數據:![]() )
)
參考時間軸:

A.戰國B.兩漢C.唐朝D.宋朝
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以平面直角坐標系
為參數),以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程及曲線
的直角坐標方程及曲線![]() 上的動點
上的動點![]() 到坐標原點
到坐標原點![]() 的距離
的距離![]() 的最大值;
的最大值;
(Ⅱ)若曲線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,且與
兩點,且與![]() 軸相交于點
軸相交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某藝術品公司欲生產一款迎新春工藝禮品,該禮品是由玻璃球面和該球的內接圓錐組成,圓錐的側面用于藝術裝飾,如圖1.為了便于設計,可將該禮品看成是由圓![]() 及其內接等腰三角形
及其內接等腰三角形![]() 繞底邊
繞底邊![]() 上的高所在直線
上的高所在直線![]() 旋轉180°而成,如圖2.已知圓
旋轉180°而成,如圖2.已知圓![]() 的半徑為
的半徑為![]() ,設
,設![]() ,圓錐的側面積為
,圓錐的側面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)為了達到最佳觀賞效果,要求圓錐的側面積![]() 最大.求
最大.求![]() 取得最大值時腰
取得最大值時腰![]() 的長度.
的長度.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com