【題目】軍訓時，甲、乙兩名同學進行射擊比賽，共比賽10場，每場比賽各射擊四次，且用每場擊中環數之和作為該場比賽的成績．數學老師將甲、乙兩名同學的10場比賽成績繪成如圖所示的莖葉圖，并給出下列4個結論：(1)甲的平均成績比乙的平均成績高；(2)甲的成績的極差是29；(3)乙的成績的眾數是21；(4)乙的成績的中位數是18．則這4個結論中，正確結論的個數為( )
A. 1B. 2C. 3D. 4
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知拋物線E：
，圓C：
．
若過拋物線E的焦點F的直線l與圓C相切，求直線l方程；
在的條件下，若直線l交拋物線E于A，B兩點，x軸上是否存在點
使
為坐標原點
？若存在，求出點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將正
分割
成個全等的小正三角形（圖1，圖2分別給出了
的情形），在每個三角形的頂點各放置一個數，使位于的三邊及平行于某邊的任一直線上的數（當數的個數不少于3時）都分別依次成等差數列，若頂點
處的三個數互不相同且和為1，記所有頂點上的數的和為
，已知
，則（用含
的式子表達）__________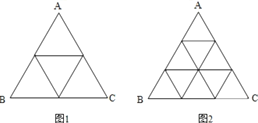
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（Ⅰ）求
的單調區間；
（Ⅱ）求在區間
上的最小值.
【答案】（Ⅰ）
;（Ⅱ）
.
【解析】（Ⅰ）
.
令
，得
.
與
的情況如上：
所以，的單調遞減區間是
，單調遞增區間是
.
（Ⅱ）當
，即
時，函數在上單調遞增，
所以在區間上的最小值為
.
當
，即
時，
由（Ⅰ）知在
上單調遞減，在
上單調遞增，
所以在區間上的最小值為
.
當
，即
時，函數在上單調遞減，
所以在區間上的最小值為
.
綜上，當時，的最小值為
；
當時，的最小值為
；
當時，的最小值為
.
【題型】解答題
【結束】
19
【題目】已知拋物線
的頂點在原點,焦點在坐標軸上，點
為拋物線
上一點.
（1）求
的方程；
（2）若點
在
上，過
作
的兩弦
與
，若
，求證: 直線
過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的左、右焦點分別為
，
，下頂點為
，
為坐標原點，點到直線
的距離為
，
為等腰直角三角形.
（1）求橢圓
的標準方程；
（2）直線
與橢圓交于
，
兩點，若直線
與直線
的斜率之和為
，證明：直線恒過定點，并求出該定點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M為線段AD上一點，AM=2MD，N為PC的中點.
（Ⅰ）證明MN∥平面PAB;
（Ⅱ）求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】世界衛生組織的最新研究報告顯示，目前中國近視患者人數多達6億，高中生和大學生的近視率均已超過七成，為了研究每周累計戶外暴露時間（單位：小時）與近視發病率的關系，對某中學一年級200名學生進行不記名問卷調查，得到如下數據：
每周累積戶外暴露時間（單位：小時） |
|
|
|
| 不少于28小時 |
近視人數 | 21 | 39 | 37 | 2 | 1 |
不近視人數 | 3 | 37 | 52 | 5 | 3 |
（1）在每周累計戶外暴露時間不少于28小時的4名學生中，隨機抽取2名，求其中恰有一名學生不近視的概率；
（2）若每周累計戶外暴露時間少于14個小時被認證為“不足夠的戶外暴露時間”，根據以上數據完成如下列聯表，并根據（2）中的列聯表判斷能否在犯錯誤的概率不超過0.01的前提下認為不足夠的戶外暴露時間與近視有關系？
近視 | 不近視 | |
足夠的戶外暴露時間 | ||
不足夠的戶外暴露時間 |
附:
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點
到定點
的距離比它到
軸的距離大
.
（1）求動點
的軌跡
的方程；
（2）設點
(
為常數)，過點
作斜率分別為
的兩條直線
與
，交曲線于
兩點，交曲線于
兩點，點
分別是線段
的中點，若
，求證：直線
過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據下列條件分別求出直線l的方程.
（1）直線l經過A（4，1），且橫、縱截距相等；
（2）直線l平行于直線3x+4y+17＝0，并且與兩坐標軸圍成的三角形的面積為24.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
