

(1)用a、b表示向量![]() 、
、![]() ;
;
(2)若![]() =λ
=λ![]() ,求實數(shù)λ的值.
,求實數(shù)λ的值.
思路分析:本題要用a、b表示![]() 、
、![]() ,而a、b不共線,由平面向量基本定理知,此平面內(nèi)任何向量都可用a、b唯一表示,因此只需結(jié)合圖形尋找
,而a、b不共線,由平面向量基本定理知,此平面內(nèi)任何向量都可用a、b唯一表示,因此只需結(jié)合圖形尋找![]() 、
、![]() 與a、b的關(guān)系即可.據(jù)向量共線條件列出與λ有關(guān)的方程,可求出λ的值.
與a、b的關(guān)系即可.據(jù)向量共線條件列出與λ有關(guān)的方程,可求出λ的值.
解:(1)∵A為BC的中點,∴![]() =
=![]() (
(![]() +
+![]() ),
),![]() =2a-b,
=2a-b,![]() =
=![]() -
-![]() =
=![]() -
-![]()
![]() =2a-b-
=2a-b-![]() b=2a-
b=2a-![]() b.
b.
(2)設(shè)![]() =λ
=λ![]() ,則
,則![]() =
=![]() -
-![]() =λ
=λ![]() -
-![]() =λa-2a+b=(λ-2)a+b.
=λa-2a+b=(λ-2)a+b.
∵![]() 與
與![]() 共線,∴存在實數(shù)m,使得
共線,∴存在實數(shù)m,使得![]() =m
=m![]() ,
,
即(λ-2)a+b=m(-2a+![]() b),
b),
即(λ+2m-2)a+(1-![]() m)b=0.
m)b=0.
∵a、b不共線,∴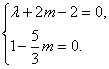 解得λ=
解得λ=![]() .
.
溫馨提示
正確運用向量加法、減法的運算法則和向量共線的條件是解決本題的關(guān)鍵.


 時刻準備著暑假作業(yè)原子能出版社系列答案
時刻準備著暑假作業(yè)原子能出版社系列答案 暑假銜接教材期末暑假預(yù)習武漢出版社系列答案
暑假銜接教材期末暑假預(yù)習武漢出版社系列答案科目:高中數(shù)學 來源: 題型:
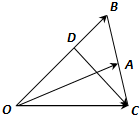
 已知△OAB中,點D在線段OB上,且OD=2DB,延長BA到C,使BA=AC.設(shè)
已知△OAB中,點D在線段OB上,且OD=2DB,延長BA到C,使BA=AC.設(shè)| OA |
| a |
| OB |
| b |
| a |
| b |
| OC |
| DC |
| OC |
| OA |
| DC |
查看答案和解析>>
科目:高中數(shù)學 來源:中學教材全解 高中數(shù)學必修4 B版(配人民教育出版社實驗教科書) 人教版 B版 題型:044
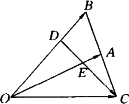
已知△OAB中,延長BA到C,使AB=AC,D是將![]() 分成2∶1的一個分點,DC和OA交于E,設(shè)
分成2∶1的一個分點,DC和OA交于E,設(shè)![]() =a,
=a,![]() =b(如圖).
=b(如圖).
(1)用a、b表示向量![]() ;
;
(2)若![]() ,求實數(shù)λ的值.
,求實數(shù)λ的值.
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
| OA |
| a |
| OB |
| b |
| a |
| b |
| OC |
| DC |
| OC |
| OA |
| DC |
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年重慶八中高一(上)期末數(shù)學試卷(解析版) 題型:解答題
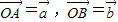 .
.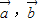 表示向量
表示向量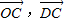 ;
;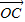 與
與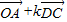 共線,求k的值.
共線,求k的值.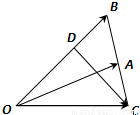
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com