
 .
.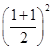 =1,
=1,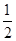 .∴a+c=
.∴a+c=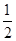 .
.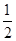 x+c≥0對x∈R恒成立.
x+c≥0對x∈R恒成立.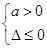 , ∴
, ∴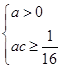 ∴c>0,故a>0,c>0.
∴c>0,故a>0,c>0.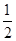 ,ac≥
,ac≥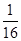 ,
,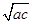 ,得ac≤
,得ac≤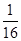 ,
,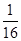 ,當且僅當a=c=
,當且僅當a=c=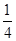 時,取“=”.
時,取“=”.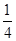 x2+
x2+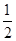 x+
x+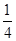 .
.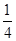 x2+
x2+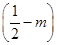 x+
x+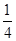
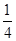 [x2+(2-4m)x+1].
[x2+(2-4m)x+1].

 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 軸上的橢圓
軸上的橢圓 的離心率為
的離心率為 ,橢圓上異于長軸頂點的任意點
,橢圓上異于長軸頂點的任意點 與左右兩焦點
與左右兩焦點 、
、 構成的三角形中面積的最大值為
構成的三角形中面積的最大值為 .
. 的標準方程;
的標準方程; ,連接
,連接 與橢圓的另一交點記為
與橢圓的另一交點記為 ,若
,若 與橢圓相切時
與橢圓相切時 、
、 不重合,連接
不重合,連接 與橢圓的另一交點記為
與橢圓的另一交點記為 ,求
,求 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 .設
.設 ,
, (max{p,q}表示p,q中的較大值,min{p,q}表示p,q中的較小值).記
(max{p,q}表示p,q中的較大值,min{p,q}表示p,q中的較小值).記 的最小值為A,
的最小值為A, 的最大值為B,則
的最大值為B,則 ( )
( )| A.16 |
B. |
C. |
D. |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 (x
(x -2x+3)有以下4個結論:其中正確的有 .
-2x+3)有以下4個結論:其中正確的有 .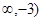
 ; ② 遞增區間為
; ② 遞增區間為 ;
; 軸的上方.
軸的上方.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com