
【題目】某廠接受了一項加工業務,加工出來的產品(單位:件)按標準分為A,B,C,D四個等級.加工業務約定:對于A級品、B級品、C級品,廠家每件分別收取加工費90元,50元,20元;對于D級品,廠家每件要賠償原料損失費50元.該廠有甲、乙兩個分廠可承接加工業務.甲分廠加工成本費為25元/件,乙分廠加工成本費為20元/件.廠家為決定由哪個分廠承接加工業務,在兩個分廠各試加工了100件這種產品,并統計了這些產品的等級,整理如下:
甲分廠產品等級的頻數分布表
等級 | A | B | C | D |
頻數 | 40 | 20 | 20 | 20 |
乙分廠產品等級的頻數分布表
等級 | A | B | C | D |
頻數 | 28 | 17 | 34 | 21 |
(1)分別估計甲、乙兩分廠加工出來的一件產品為A級品的概率;
(2)分別求甲、乙兩分廠加工出來的100件產品的平均利潤,以平均利潤為依據,廠家應選哪個分廠承接加工業務?
科目:高中數學 來源: 題型:
【題目】已知![]() 的內角A,B,C所對的邊分別是a,b,c,其面積S
的內角A,B,C所對的邊分別是a,b,c,其面積S![]() .
.
(1)若a![]() ,b
,b![]() ,求cosB.
,求cosB.
(2)求sin(A+B)+sinBcosB+cos(B﹣A)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三位同學進行羽毛球比賽,約定賽制如下:累計負兩場者被淘汰;比賽前抽簽決定首先比賽的兩人,另一人輪空;每場比賽的勝者與輪空者進行下一場比賽,負者下一場輪空,直至有一人被淘汰;當一人被淘汰后,剩余的兩人繼續比賽,直至其中一人被淘汰,另一人最終獲勝,比賽結束.經抽簽,甲、乙首先比賽,丙輪空.設每場比賽雙方獲勝的概率都為![]() ,
,
(1)求甲連勝四場的概率;
(2)求需要進行第五場比賽的概率;
(3)求丙最終獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱ABC–A1B1C1的底面是正三角形,側面BB1C1C是矩形,M,N分別為BC,B1C1的中點,P為AM上一點.過B1C1和P的平面交AB于E,交AC于F.
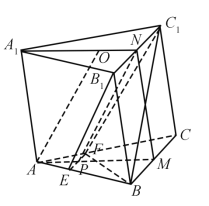
(1)證明:AA1//MN,且平面A1AMN⊥平面EB1C1F;
(2)設O為△A1B1C1的中心,若AO=AB=6,AO//平面EB1C1F,且∠MPN=![]() ,求四棱錐B–EB1C1F的體積.
,求四棱錐B–EB1C1F的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() 且橢圓的短軸長為
且橢圓的短軸長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知動直線![]() 過右焦點
過右焦點![]() ,且與橢圓
,且與橢圓![]() 分別交于
分別交于![]() 兩點.試問
兩點.試問![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得,
,使得,![]() 恒成立?若存在求出點
恒成立?若存在求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義城為R的函數![]() ,若滿足:①
,若滿足:①![]() ;②當
;②當![]() ,且
,且![]() 時,都有
時,都有![]() ;③當
;③當![]() 且
且![]() 時,都有
時,都有![]() ,則稱
,則稱![]() 為“偏對稱函數”.下列函數是“偏對稱函數”的是( )
為“偏對稱函數”.下列函數是“偏對稱函數”的是( )
A.![]() B.
B.![]()
C.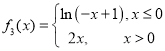 D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com