
已知 ,
,
(1)當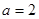 時,解不等式
時,解不等式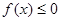 ;
;
(2)若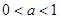 ,解關于
,解關于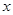 的不等式
的不等式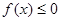 。
。
科目:高中數學 來源: 題型:解答題
設p:函數y=loga(x+1)(a>0且a≠1)在(0,+∞)上單調遞減; q:曲線y=x2+(2a-3)x+1與x軸交于不同的兩點.如果p∧q為假,p∨q為真,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知m∈R,對p:x1和x2是方程x2-ax-2=0的兩個根,不等式|m-5|≤|x1-x2|對任意實數a∈[1,2]恒成立;q:函數f(x)=3x2+2mx+m+ 有兩個不同的零點.求使“p且q”為假命題、“p或q”為真命題的實數m的取值范圍.
有兩個不同的零點.求使“p且q”為假命題、“p或q”為真命題的實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
養路處建造無底的圓錐形倉庫用于貯藏食鹽(供融化高速公路上的積雪之用),已建的倉庫的底面直徑為12米,高4米。養路處擬另建一個更大的圓錐形倉庫,以存放更多食鹽。現有兩種方案:一是新建的倉庫的底面直徑比原來增加4米(高不變);二是高度增加4米(底面直徑不變)。
分別計算按這兩種方案所建的倉庫的體積;
分別計算按這兩種方案所建的倉庫的表面積;
哪個方案更經濟些?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地區注重生態環境建設,每年用于改造生態環境總費用為 億元,其中用于風景區改造為
億元,其中用于風景區改造為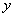 億元。該市決定建立生態環境改造投資方案,該方案要求同時具備下列三個條件:①每年用于風景區改造費用隨每年改造生態環境總費用增加而增加;②每年改造生態環境總費用至少
億元。該市決定建立生態環境改造投資方案,該方案要求同時具備下列三個條件:①每年用于風景區改造費用隨每年改造生態環境總費用增加而增加;②每年改造生態環境總費用至少 億元,至多
億元,至多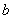 億元;③每年用于風景區改造費用不得低于每年改造生態環境總費用的15%,但不得每年改造生態環境總費用的22%。
億元;③每年用于風景區改造費用不得低于每年改造生態環境總費用的15%,但不得每年改造生態環境總費用的22%。
(1)若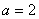 ,
,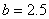 ,請你分析能否采用函數模型y=
,請你分析能否采用函數模型y=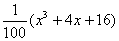 作為生態環境改造投資方案;
作為生態環境改造投資方案;
(2)若 、
、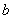 取正整數,并用函數模型y=
取正整數,并用函數模型y=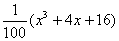 作為生態環境改造投資方案,請你求出
作為生態環境改造投資方案,請你求出 、
、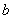 的取值.
的取值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位決定對本單位職工實行年醫療費用報銷制度,擬制定年醫療總費用在2萬元至10萬元(包括2萬元和10萬元)的報銷方案,該方案要求同時具備下列三個條件:①報銷的醫療費用y(萬元)隨醫療總費用x(萬元)增加而增加;②報銷的醫療費用不得低于醫療總費用的50%;③報銷的醫療費用不得超過8萬元.
(1)請你分析該單位能否采用函數模型y=0.05(x2+4x+8)作為報銷方案;
(2)若該單位決定采用函數模型y=x-2lnx+a(a為常數)作為報銷方案,請你確定整數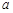 的值.(參考數據:ln2»0.69,ln10»2.3)
的值.(參考數據:ln2»0.69,ln10»2.3)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知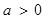 ,函數
,函數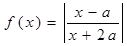 。
。
(I)記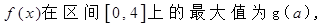 求
求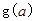 的表達式;
的表達式;
(II)是否存在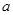 ,使函數
,使函數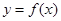 在區間
在區間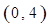 內的圖像上存在兩點,在該兩點處的切線相互垂直?若存在,求
內的圖像上存在兩點,在該兩點處的切線相互垂直?若存在,求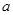 的取值范圍;若不存在,請說明理由。
的取值范圍;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com