
已知函數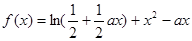 。(
。(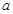 為常數,
為常數, )
)
(Ⅰ)若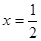 是函數
是函數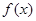 的一個極值點,求
的一個極值點,求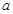 的值;
的值;
(Ⅱ)求證:當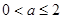 時,
時,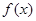 在
在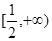 上是增函數;
上是增函數;
(Ⅲ)若對任意的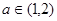 ,總存在
,總存在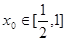 ,使不等式
,使不等式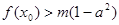 成立,求實數
成立,求實數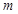 的取值范圍。
的取值范圍。
(Ⅰ)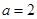 ;(Ⅱ)詳見解析;(Ⅲ)實數
;(Ⅱ)詳見解析;(Ⅲ)實數 的取值范圍為
的取值范圍為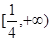
【解析】
試題分析:(Ⅰ)函數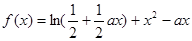 ,
, 是函數
是函數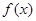 的一個極值點,先求出其導函數:
的一個極值點,先求出其導函數: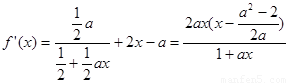 ,利用
,利用 是函數
是函數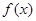 的一個極值點對應的結論,即
的一個極值點對應的結論,即 時,它的導函數值為零,可令
時,它的導函數值為零,可令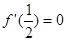 ,即可求
,即可求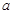 的值;(Ⅱ)求證:當
的值;(Ⅱ)求證:當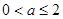 時,
時,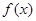 在
在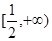 上是增函數,由于
上是增函數,由于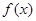 含有對數函數,可通過求導來證明,因此利用:
含有對數函數,可通過求導來證明,因此利用: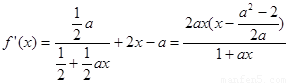 ,在
,在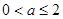 時,分析出因式中的每一項都大于等于0,即得
時,分析出因式中的每一項都大于等于0,即得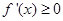 ,從而可證明結論;(Ⅲ)先由(Ⅱ)知,
,從而可證明結論;(Ⅲ)先由(Ⅱ)知,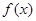 在
在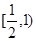 上的最大值為
上的最大值為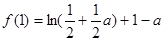 ,把問題轉化為對任意的
,把問題轉化為對任意的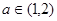 ,不等式
,不等式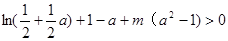 恒成立;然后再利用導函數研究不等式左邊的最小值看是否符合要求即可求實數
恒成立;然后再利用導函數研究不等式左邊的最小值看是否符合要求即可求實數 的取值范圍為
的取值范圍為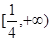 .
.
試題解析: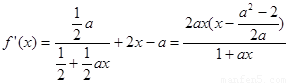
(Ⅰ)由已知,得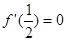 且
且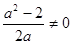 ,
,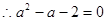
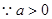
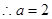 3分
3分
(Ⅱ)當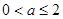 時,
時,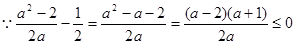
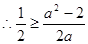
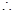 當
當 時,
時,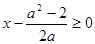 又
又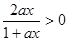
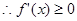
故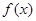 在
在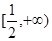 上是增函數
6分
上是增函數
6分
(Ⅲ)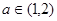 時,由(Ⅱ)知,
時,由(Ⅱ)知,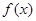 在
在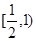 上的最大值為
上的最大值為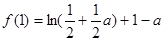
于是問題等價于:對任意的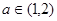 ,不等式
,不等式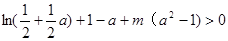 恒成立。
恒成立。
記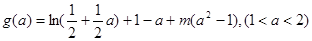
則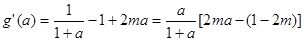
當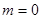 時,
時,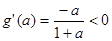
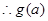 在區間
在區間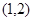 上遞減,此時
上遞減,此時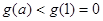
由于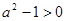 ,
,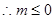 時不可能使
時不可能使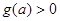 恒成立,故必有
恒成立,故必有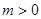
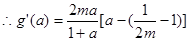
若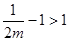 ,可知
,可知 在區間
在區間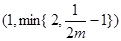 上遞減,在此區間上,有
上遞減,在此區間上,有
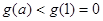 ,與
,與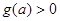 恒成立相矛盾,故
恒成立相矛盾,故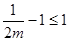 ,這時
,這時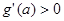 ,
,
 在
在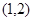 上遞增,恒有
上遞增,恒有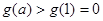 ,滿足題設要求,
,滿足題設要求,
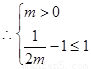 即
即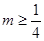
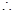 實數
實數 的取值范圍為
的取值范圍為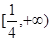 14分
14分
考點:利用導數研究函數的極值,導數在最大值、最小值問題中的應用.


科目:高中數學 來源: 題型:
(09年江寧中學三月)(16分)已知函數![]() ,
,![]() (
(![]() 為常數).函數
為常數).函數![]() 定義為:對每個給定的實數
定義為:對每個給定的實數![]() ,
,![]()
(1)求![]() 對所有實數
對所有實數![]() 成立的充分必要條件(用
成立的充分必要條件(用![]() 表示);
表示);
(2)設![]() 是兩個實數,滿足
是兩個實數,滿足![]() ,且
,且![]() .若
.若![]() ,求證:函數
,求證:函數![]() 在區間
在區間![]() 上的單調增區間的長度之和為
上的單調增區間的長度之和為![]() (閉區間
(閉區間![]() 的長度定義為
的長度定義為![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題12分)已知函數![]() (m為常數,m>0)有極大值9.
(m為常數,m>0)有極大值9.
(1)求m的k*s#5^u值;
(2)若斜率為-5的k*s#5^u直線是曲線![]() 的k*s#5^u切線,求此直線方程.
的k*s#5^u切線,求此直線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com