
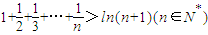 ;
;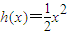 ,試探究函數f(x)與h(x)是否存在“分界線”?若存在,請加以證明,并求出k,b的值;若不存在,請說明理由.
,試探究函數f(x)與h(x)是否存在“分界線”?若存在,請加以證明,并求出k,b的值;若不存在,請說明理由.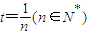 ,原問題轉化成一個數列問題解決.
,原問題轉化成一個數列問題解決.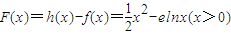 ,原問題轉化為研究此函數的單調性問題,利用導數知識解決.
,原問題轉化為研究此函數的單調性問題,利用導數知識解決.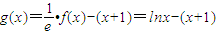 ,∴
,∴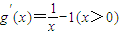 .(1分)
.(1分)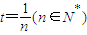 ,
,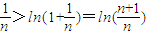 ,(7分)
,(7分)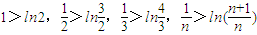 ,
, (8分)
(8分)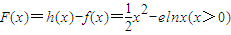 ,
,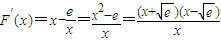 .
.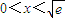 時,F′(x)<0,函數F(x)單調遞減;
時,F′(x)<0,函數F(x)單調遞減;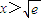 時,F′(x)>0,函數F(x)單調遞增.
時,F′(x)>0,函數F(x)單調遞增.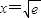 是函數F(x)的極小值點,也是最小值點,∴
是函數F(x)的極小值點,也是最小值點,∴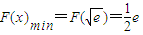
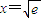 處有公共點
處有公共點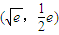 .(9分)
.(9分)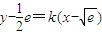 .
.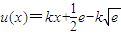 ,
, 在x∈R恒成立,
在x∈R恒成立,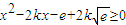 在R上恒成立,
在R上恒成立,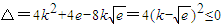 成立,
成立,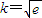 ,故
,故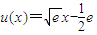 .(11分)
.(11分) 恒成立.
恒成立.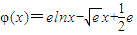 ,則
,則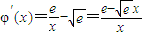 .
.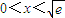 時,φ′(x)>0,函數φ(x)單調遞增;當
時,φ′(x)>0,函數φ(x)單調遞增;當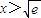 時,φ′(x)<0.函數φ(x)單調遞減.
時,φ′(x)<0.函數φ(x)單調遞減.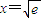 時φ(x)取得最大值0,則
時φ(x)取得最大值0,則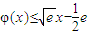 (x>0)成立.(13分)
(x>0)成立.(13分)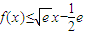 且
且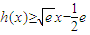 ,
,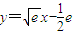 ,此時
,此時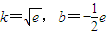 .(14分)
.(14分)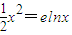 ,探究得兩函數圖象的交點為
,探究得兩函數圖象的交點為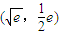 ,
,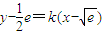 ,令函數
,令函數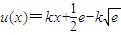 ,
,

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com