
【題目】如圖,底面![]() 是邊長為2且
是邊長為2且![]() 的菱形,
的菱形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
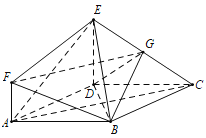
(1)求證:平面![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,且三棱錐
上,且三棱錐![]() 的體積是三棱錐
的體積是三棱錐![]() 的體積的兩倍,求二面角
的體積的兩倍,求二面角![]() 的正弦值.
的正弦值.
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,橢圓C:
中,橢圓C:![]() 的離心率是
的離心率是![]() ,拋物線E:
,拋物線E:![]() 的焦點F是C的一個頂點.
的焦點F是C的一個頂點.
(Ⅰ)求橢圓C的方程;
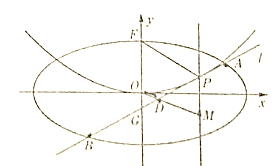
(Ⅱ)設P是E上的動點,且位于第一象限,E在點P處的切線![]() 與C交與不同的兩點A,B,線段AB的中點為D,直線OD與過P且垂直于x軸的直線交于點M.
與C交與不同的兩點A,B,線段AB的中點為D,直線OD與過P且垂直于x軸的直線交于點M.
(i)求證:點M在定直線上;
(ii)直線![]() 與y軸交于點G,記
與y軸交于點G,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值及取得最大值時點P的坐標.
的最大值及取得最大值時點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】狄利克雷函數是高等數學中的一個典型函數,若![]() ,則稱
,則稱![]() 為狄利克雷函數.對于狄利克雷函數
為狄利克雷函數.對于狄利克雷函數![]() ,給出下面4個命題:①對任意
,給出下面4個命題:①對任意![]() ,都有
,都有![]() ;②對任意
;②對任意![]() ,都有
,都有![]() ;③對任意
;③對任意![]() ,都有
,都有![]() ,
, ![]() ;④對任意
;④對任意![]() ,都有
,都有![]() .其中所有真命題的序號是( )
.其中所有真命題的序號是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左右頂點分別為
的左右頂點分別為![]() ,
,![]() ,點
,點![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的任意一點,設直線
的任意一點,設直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,且
,且![]() ,橢圓的焦距長為4.
,橢圓的焦距長為4.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過右焦點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,分別記
兩點,分別記![]() ,
,![]() 的面積為
的面積為![]() 、
、![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,將
的中點,將![]() 沿
沿![]() 翻折,構成一個四棱錐
翻折,構成一個四棱錐![]() ,如圖2.
,如圖2.
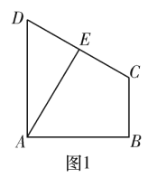
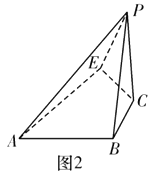
(1)求證:異面直線![]() 與
與![]() 垂直;
垂直;
(2)求直線![]() 與平面
與平面![]() 所成角的大小;
所成角的大小;
(3)若三棱錐![]() 的體積為
的體積為![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學著作《算法統宗》中記載了這樣的一個問題:“三百七十八里關,初行健步不為難,次日腳痛減一半,六朝才得到其關,要見次日行里數,請公仔細算相還”,其大意為:有一個人走了378里路,第一天健步行走,從第二天起其因腳痛每天走的路程為前一天的一半,走了6天后到達了目的地,問此人第三天走的路程里數為( )
A.192B.48C.24D.88
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的坐標為
的坐標為![]() ,若點
,若點![]() 是曲線
是曲線![]() 截直線
截直線![]() 所得線段的中點,求
所得線段的中點,求![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com