Question

（05年浙江卷文）（14分）

已知函數和的圖象關于原點對稱，且．

   (Ⅰ)求函數的解析式；

   (Ⅱ)解不等式；

   (Ⅲ)若在上是增函數，求實數的取值范圍．

Answer 1

解析：(Ⅰ)設函數y=f(x)的圖象上任一點Q(x_qλ,y_q關于原點的對稱點(x,y),

則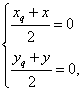即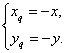∵點Qx_q,y_q)在函數f(x)的圖象上,

∴-y=-x²+2x.,故g(x)=-x²+2x

(Ⅱ)由g(x)≥f(x)－|x－1|可得2x²-|x-1|≤0,當x≥1時,2x²-x+1≤0,此時不等式無解,

當x<1時,2x²+x-1≤0,∴-1≤x≤,因此,原不等式的解集為[-1,]

(Ⅲ)h(x)=-(1+λ)x²+2(1-λ)x+1

①     當λ=-1時,h(x)=4x+1在[-1,1]上是增函數,∴λ=-1

②     當λ≠-1時,對稱軸的方程為x=.

(i)                  當λ<-1時, ≤-1,解得λ<-1.

(ii)                當λ>-1時, ≥-1,解得-1<λ≤0.

綜上,λ≤0