
 經過點P(2,1),離心率
經過點P(2,1),離心率 ,直線l與橢圓C交于A,B兩點 (A,B均異于點P),且有
,直線l與橢圓C交于A,B兩點 (A,B均異于點P),且有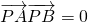 .
.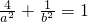 ,
, ,a2=b2+c2,
,a2=b2+c2,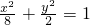 .
.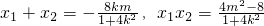 .
.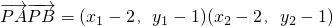 =(x1-2)(x2-2)+(y1-1)(y2-1)=(x1-2)(x2-2)+(kx1+m-1)(kx2+m-1)
=(x1-2)(x2-2)+(y1-1)(y2-1)=(x1-2)(x2-2)+(kx1+m-1)(kx2+m-1)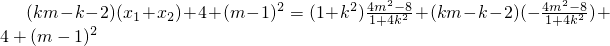
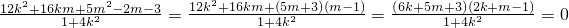
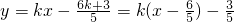 ,∴直線l過定點
,∴直線l過定點 .
. ,符合題意.
,符合題意.
 ,a2=b2+c2,可解出a,b,c.
,a2=b2+c2,可解出a,b,c. =
=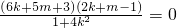
 ,符合題意.
,符合題意.

科目:高中數學 來源:2011年陜西省寶雞市金臺區高三質量檢測數學試卷(解析版) 題型:解答題
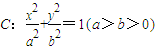 經過點P(2,1),離心率
經過點P(2,1),離心率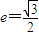 ,直線l與橢圓C交于A,B兩點 (A,B均異于點P),且有
,直線l與橢圓C交于A,B兩點 (A,B均異于點P),且有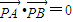 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com