【題目】已知函數
，其中
為常數．
(1)若
，求函數
的極值；
(2)若函數在
上單調遞增，求實數的取值范圍．
【答案】（1）見解析；（2）
.
【解析】分析：求出
，在定義域內，分別令
求得
的范圍，可得函數
增區間，
求得的范圍，可得函數的減區間，利用函數的單調性可求出函數的極值；（2）
在
上單調遞增等價于
在
上恒成立，求得導數和單調區間，討論
與極值點的關系，結合單調性，運用參數分離和解不等式可得
范圍.
詳解：（1）當
時：
的定義域為
令
，得
當
時，
，在
上單調遞增；
當
時，
，在
上單調遞減；
當時，的極大值為
，無極小值.
（2）
在上單調遞增
在上恒成立，
只需
在上恒成立
在上恒成立
令
則
令
，則：
①若
即
時
在上恒成立
在上單調遞減
， 
這與
矛盾，舍去
②若
即
時
當
時，，在
上單調遞減；
當
時，
，在
上單調遞增；
當時，有極小值，也是最小值，
綜上
科目：高中數學 來源： 題型：
【題目】如圖所示，在正方體
中，側面對角線
，
上分別有一點E，F，且
，則直線EF與平面ABCD所成的角的大小為（ ）
A.0°B.60°C.45°D.30°
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設甲、乙、丙三個乒乓球協會分別選派3，1，2名運動員參加某次比賽，甲協會運動員編號分別為
，
，
，乙協會編號為
，丙協會編號分別為
，
，若從這6名運動員中隨機抽取2名參加雙打比賽.
（1）用所給編號列出所有可能抽取的結果；
（2）求丙協會至少有一名運動員參加雙打比賽的概率；
（3）求參加雙打比賽的兩名運動員來自同一協會的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一塊各面均涂有油漆的正方體被鋸成27個大小相同的小正方體，若將這些小正方體均勻地攪混在一起，從中任意取出一個，則取出的小正方體兩面涂有油漆的概率是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD的底面ABCD是正方形，PD⊥平面ABCD，E為PB上的點，且2BE=EP．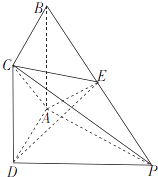 
（1）證明：AC⊥DE；
（2）若PC= 
BC，求二面角E﹣AC﹣P的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知關于
與
有表格中的數據，且與線性相關，由最小二乘法得
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
（1）求與的線性回歸方程；
（2）現有第二個線性模型：
，且
.若與（1）的線性模型比較，哪一個線性模型擬合效果比較好，請說明理由
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國古代數學名著《九章算術》中“竹九節”問題曰：“今有竹九節，下三節容量四升，上四節容量三升，問中間兩節欲均容各多少？”其意為：“現有一根9節的竹子，自上而下的容積成等差數列，下面3節容量為4升，上面4節容積為3升，問中間2節各多少容積？”則中間2節容積合計________升
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
