
【題目】如圖所示,三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 和
和![]() 邊上的點,且
邊上的點,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
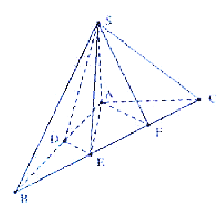
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見證明;(2) ![]()
【解析】
(1)在![]() 中,根據余弦定理,可得
中,根據余弦定理,可得![]() ,所以
,所以![]() ,即
,即![]() 是直角三角形,又
是直角三角形,又![]() 為
為![]() 的中點,所以
的中點,所以![]() 為等邊三角形,根據線面平行的判定定理即可證明。
為等邊三角形,根據線面平行的判定定理即可證明。
(2)以點![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建系,求出
軸建系,求出![]() ,平面
,平面![]()
法向量![]() 的坐標,計算
的坐標,計算![]() 與法向量
與法向量![]() 的夾角,可得所求。
的夾角,可得所求。
(1)平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
則![]() 平面
平面![]() ,
,
又![]() ,則
,則![]()
因為![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]()
由余弦定理可得:![]()
解得:![]()
所以![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
又![]() 為
為![]() 的中點,所以
的中點,所以![]()
又![]() ,所以
,所以![]() 為等邊三角形,
為等邊三角形,
所以![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由(1)可知![]() ,以點
,以點![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標系,則
軸建立空間直角坐標系,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
設![]() 為平面
為平面![]() 的法向量,則
的法向量,則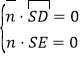 ,即
,即![]()
設![]() ,則
,則![]() ,
,![]() ,即平面
,即平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以![]() ,
,![]()
![]()
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】近年來,隨著互聯網技術的快速發展,共享經濟覆蓋的范圍迅速擴張,繼共享單車、共享汽車之后,共享房屋以“民宿”、“農家樂”等形式開始在很多平臺上線.某創業者計劃在某景區附近租賃一套農房發展成特色“農家樂”,為了確定未來發展方向,此創業者對該景區附近六家“農家樂”跟蹤調查了![]() 天.得到的統計數據如下表,
天.得到的統計數據如下表,![]() 為收費標準(單位:元/日),
為收費標準(單位:元/日),![]() 為入住天數(單位:),以頻率作為各自的“入住率”,收費標準
為入住天數(單位:),以頻率作為各自的“入住率”,收費標準![]() 與“入住率”
與“入住率”![]() 的散點圖如圖
的散點圖如圖
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
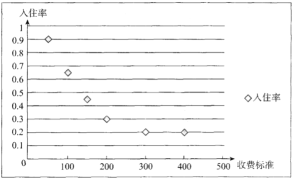
(1)若從以上六家“農家樂”中隨機抽取兩家深入調查,記![]() 為“入住率”超過
為“入住率”超過![]() 的農家樂的個數,求
的農家樂的個數,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散點圖判斷
,由散點圖判斷![]() 與
與![]() 哪個更合適于此模型(給出判斷即可,不必說明理由)?并根據你的判斷結果求回歸方程.(
哪個更合適于此模型(給出判斷即可,不必說明理由)?并根據你的判斷結果求回歸方程.(![]() 結果保留一位小數)
結果保留一位小數)
(3)若一年按![]() 天計算,試估計收費標準為多少時,年銷售額
天計算,試估計收費標準為多少時,年銷售額![]() 最大?(年銷售額
最大?(年銷售額![]() 入住率
入住率![]() 收費標準
收費標準![]() )
)
參考數據: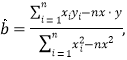
![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 截直線
截直線![]() 所得的線段的長度為
所得的線段的長度為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 上的點,
上的點,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() :
:![]() 經過點
經過點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 是橢圓
是橢圓![]() 上的任意一點,射線
上的任意一點,射線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點,直線
有且只有一個公共點,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩個相異點,證明:
兩個相異點,證明:![]() 面積為定值.
面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,DC⊥平面ABC,![]() ,
,![]() ,
,![]() ,P、Q分別為AE,AB的中點.
,P、Q分別為AE,AB的中點.
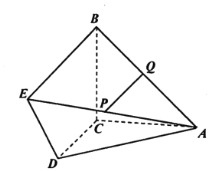
(1)證明:![]() 平面
平面![]() .
.
(2)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)求平面![]() 與平面
與平面![]() 所成銳二面角的大小。
所成銳二面角的大小。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為中心,以坐標軸為對稱軸的幫圓C經過點M(2,1),N .
.
(1)求橢圓C的標準方程;
(2)經過點M作傾斜角互補的兩條直線,分別與橢圓C相交于異于M點的A,B兩點,當△AMB面積取得最大值時,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,設橢圓
中,設橢圓![]() 的左焦點為
的左焦點為![]() ,左準線為
,左準線為![]() 為橢圓
為橢圓![]() 上任意一點,直線
上任意一點,直線![]() ,垂足為
,垂足為![]() ,直線
,直線![]() 與
與![]() 交于點
交于點![]() .
.
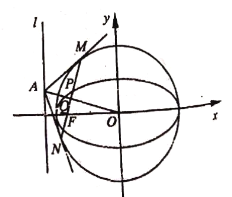
(1)若![]() ,且
,且![]() ,直線
,直線![]() 的方程為
的方程為![]() .①求橢圓
.①求橢圓![]() 的方程;②是否存在點
的方程;②是否存在點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
(2)設直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,求證:直線
兩點,求證:直線![]() 均與圓
均與圓![]() 相切.
相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E為AB的中點,P為以A為圓心、AB為半徑的圓弧上的任意一點,設向量![]() =λ
=λ![]() +μ
+μ![]() ,則λ+μ的最小值為( )
,則λ+μ的最小值為( )
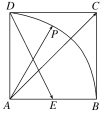
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com