Question

【題目】某市四所重點中學進行高二期中聯考，共有5000名學生參加，為了了解數學學科的學習情況，現從中隨機地抽出若干名學生在這次測試中的數學成績，制成如下頻率分布表：

分組	頻數	頻率
	①	②
		0.050
		0.200
	36	0.300
		0.275
	12	③
		0.050
合計		④

（1）根據上面的頻率分布表，推出①②③④處的數字分別為 ， ， ， .

（2）補全上的頻率分布直方圖.

（3）根據題中的信息估計總體：

①成績在120分及以上的學生人數；

②成績在的頻率.

Answer 1

【答案】（1）3; 0.025; 0.100; 1（2）見解析（3）;

【解析】

（1）根據頻率與頻數關系,可先求得③;再根據④對應的數字為1,可求得②,再求得①即可.

（2）結合頻率分布表,即可求得各組對應的,即可畫出頻率分布直方圖.

（3）由頻率分布表可知成績在120分及以上的頻率,結合總體數量即可得解;將內各組的頻率求和,即可得成績在的頻率.

（1）在內的人數為36人,頻率為0.300.

所以抽取的人數為人

在有12人,所以對應的頻率為,故③對應的數字為0.100;

根據所有頻率和為1,可知④對應的數字為1.則②對應的數字為

所以①對應的人數為

故①②③④處的數字分別為3; 0.025; 0.100; 1

（2）根據頻率分布表,可得頻率分布直方圖如下圖所示:

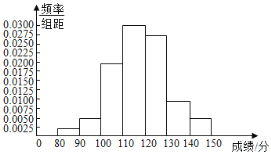
（3）①根據頻率分布表及抽取總人數為120,可得成績在120分及以上的學生人數為

人

②根據頻率分布表,將內各組的頻率求和可得