
 ,|
,| |=1.則函數y=
|=1.則函數y= 的最大值為 .
的最大值為 .  ,再表示出函數y的表達式整理得到y=282+2(cos
,再表示出函數y的表達式整理得到y=282+2(cos ,sin
,sin )
)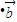 ,最后根據向量模的運算和三角函數的取值范圍確定最終答案.
,最后根據向量模的運算和三角函數的取值范圍確定最終答案.

 +
+ +2
+2 +…+
+…+ +
+ +2
+2
 )
)
 +cos
+cos +…cos
+…cos ,sin
,sin +sin
+sin +…sin
+…sin )
)
 ,sin
,sin )
)
 ,sin
,sin )
) =|(cos
=|(cos ,sin
,sin )||
)|| |cosθ(θ為向量(cos
|cosθ(θ為向量(cos ,sin
,sin )與向量
)與向量 的夾角)
的夾角) ,sin
,sin )||
)|| |=1
|=1

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com