【答案】
分析:(1)由
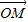
=

(
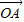
+
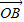
)知M為線段AB的中點,由M的橫坐標為

得x
1+x
2=1,由此可求得y
1+y
2,從而可得點M的縱坐標;
(2)根據S
n=f(
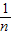
)+f(
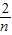
)+…+f(
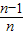
),分別令n=2,3,4即可求得s
2,s
3,s
4;由(1)知,由
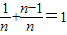
,得f(
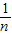
)+f(
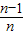
)=1,從而可求得2S
n;
(3)先表示出a
n,利用裂項相消法求得T
n,分離出參數λ后轉化為求函數的最值可解決,利用基本不等式可得最值;
解答:解:(1)依題意,由
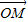
=

(
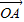
+
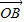
)知M為線段AB的中點,
又因為M的橫坐標為

,A(x
1,y
1),B(x
2,y
2),
∴
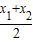
=

,即x
1+x
2=1,
∴
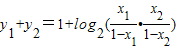
=1+log
21=1,
所以
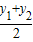
=

,
即點M的橫坐標為定值

;
(2)
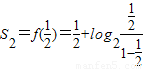
=

,
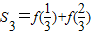
=
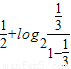
+
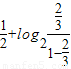
=1,
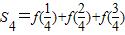
=
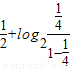
+
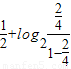
+
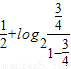
=

,
由(1)知,由
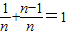
,得f(
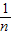
)+f(
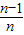
)=1,
又S
n=f(
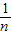
)+f(
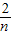
)+…+f(
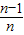
)=f(
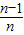
)+f(
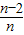
)+…+f(
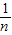
),
所以2S
n=(n-1)×1,即S
n=
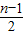
(n∈N
*且n≥2);
(3)當n≥2時,
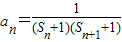
=
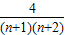
,
又n=1時,
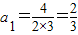
也適合,
所以
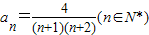
,
∴
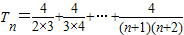
=4(
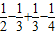
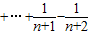
)
=4(
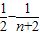
)=
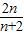
(n∈N*),
由
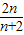
≤λ
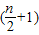
恒成立(n∈N*)推得λ≥
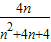
,
而
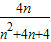
=
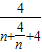
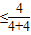
=

(當且僅當n=2取等號),
∴
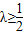
,∴λ的最小正整數為1.
點評:本題考查數列與不等式、數列與向量的綜合,考查恒成立問題,考查轉化思想,綜合性強,難度較大.

 +log2
+log2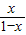 圖象上任意兩點,且
圖象上任意兩點,且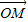 =
= (
(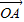 +
+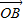 ),已知點M的橫坐標為
),已知點M的橫坐標為 ,且有Sn=f(
,且有Sn=f(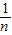 )+f(
)+f(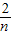 )+…+f(
)+…+f(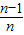 ),其中n∈N*且n≥2,
),其中n∈N*且n≥2,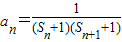 ,其中n∈N*,且Tn為數列{an}的前n項和,若Tn≤λ(Sn+1+1)對一切n∈N*都成立,試求λ的最小正整數值.
,其中n∈N*,且Tn為數列{an}的前n項和,若Tn≤λ(Sn+1+1)對一切n∈N*都成立,試求λ的最小正整數值.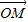 =
= (
(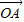 +
+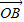 )知M為線段AB的中點,由M的橫坐標為
)知M為線段AB的中點,由M的橫坐標為 得x1+x2=1,由此可求得y1+y2,從而可得點M的縱坐標;
得x1+x2=1,由此可求得y1+y2,從而可得點M的縱坐標;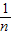 )+f(
)+f(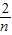 )+…+f(
)+…+f(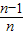 ),分別令n=2,3,4即可求得s2,s3,s4;由(1)知,由
),分別令n=2,3,4即可求得s2,s3,s4;由(1)知,由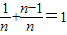 ,得f(
,得f(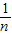 )+f(
)+f(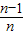 )=1,從而可求得2Sn;
)=1,從而可求得2Sn;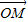 =
= (
(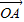 +
+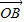 )知M為線段AB的中點,
)知M為線段AB的中點, ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),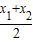 =
= ,即x1+x2=1,
,即x1+x2=1,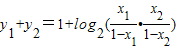 =1+log21=1,
=1+log21=1,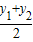 =
= ,
, ;
;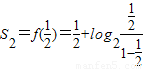 =
= ,
,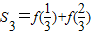 =
=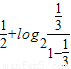 +
+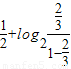 =1,
=1,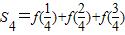 =
=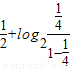 +
+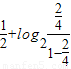 +
+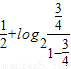 =
= ,
,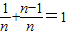 ,得f(
,得f(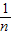 )+f(
)+f(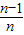 )=1,
)=1,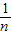 )+f(
)+f(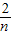 )+…+f(
)+…+f(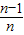 )=f(
)=f(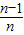 )+f(
)+f(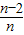 )+…+f(
)+…+f(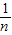 ),
),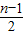 (n∈N*且n≥2);
(n∈N*且n≥2);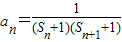 =
=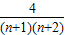 ,
,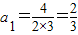 也適合,
也適合,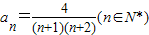 ,
,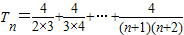 =4(
=4(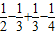
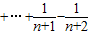 )
)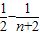 )=
)=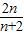 (n∈N*),
(n∈N*),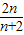 ≤λ
≤λ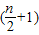 恒成立(n∈N*)推得λ≥
恒成立(n∈N*)推得λ≥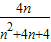 ,
,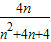 =
=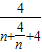
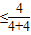 =
= (當且僅當n=2取等號),
(當且僅當n=2取等號),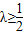 ,∴λ的最小正整數為1.
,∴λ的最小正整數為1.

 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案