
設項數均為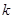 (
(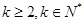 )的數列
)的數列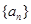 、
、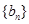 、
、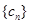 前
前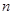 項的和分別為
項的和分別為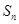 、
、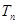 、
、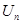 .已知
.已知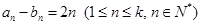 ,且集合
,且集合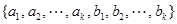 =
=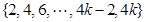 .
.
(1)已知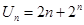 ,求數列
,求數列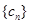 的通項公式;
的通項公式;
(2)若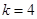 ,求
,求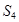 和
和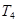 的值,并寫出兩對符合題意的數列
的值,并寫出兩對符合題意的數列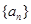 、
、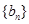 ;
;
(3)對于固定的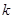 ,求證:符合條件的數列對(
,求證:符合條件的數列對(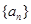 ,
,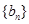 )有偶數對.
)有偶數對.
(1)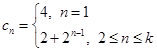 ;(2)
;(2)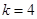 時,數列
時,數列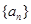 、
、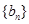 可以為(不唯一)6,12,16,14;2,8,10,4,
可以為(不唯一)6,12,16,14;2,8,10,4,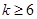 時,數列對(
時,數列對(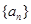 ,
,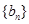 )不存在.(3)證明見解析.
)不存在.(3)證明見解析.
解析試題分析:(1)這實質是已知數列的前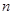 項和
項和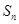 ,要求通項公式
,要求通項公式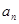 的問題,利用關系
的問題,利用關系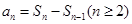 來解決;
來解決;
(2)注意到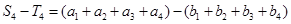
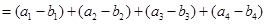 ,從而
,從而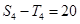 ,又
,又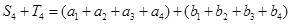
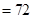 ,故可求出
,故可求出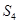 ,
, ,這里我們應用了整體思維的思想,而要寫出數列對(
,這里我們應用了整體思維的思想,而要寫出數列對(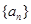 ,
,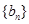 ),可通過列舉法寫出;(3)可通過構造法說明滿足題意和數列對是成對出現的,即對于數列對(
),可通過列舉法寫出;(3)可通過構造法說明滿足題意和數列對是成對出現的,即對于數列對(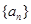 ,
,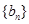 ),構造新數列對
),構造新數列對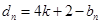 ,
,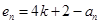 (
(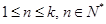 ),則數列對(
),則數列對(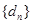 ,
,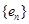 )也滿足題意,(要說明的是
)也滿足題意,(要說明的是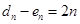 及
及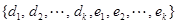 =
=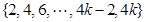 且數列
且數列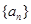 與
與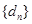 ,
,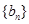 與
與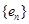 不相同(用反證法,若相同,則
不相同(用反證法,若相同,則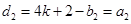 ,又
,又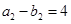 ,則有
,則有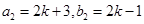 均為奇數,矛盾).
均為奇數,矛盾).
試題解析:(1)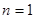 時,
時,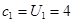
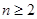 時,
時,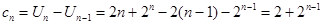 ,
,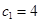 不適合該式
不適合該式
故,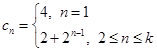 4分
4分
(2)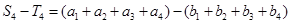
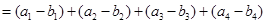
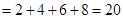
又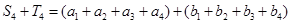

得,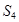 =46,
=46,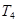 =26 8分
=26 8分
數列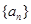 、
、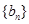 可以為:
可以為:
① 16,10,8,12;14,6,2,4 ② 14,6,10,16;12,2,4,8
③ 6,16,14,10;4,12,8,2 ④ 4,14,12,16;2,10,6,8
⑤ 4,12,16,14;2,8,10,6 ⑥ 16,8,12,10;14,4,6,2 10分
(3)令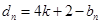 ,
,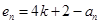 (
(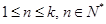 ) 12分
) 12分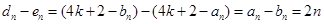
又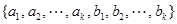 =
=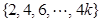 ,得
,得
=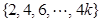
所以,數列對(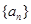 ,
,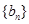 )與(
)與(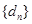 ,
,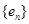 )成對出現。 16分
)成對出現。 16分
假設數列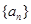 與
與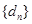 相同,則由
相同,則由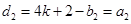 及
及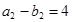 ,得
,得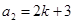 ,
,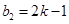 ,均為奇數
,均為奇數


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:填空題
一種計算裝置,有一個數據入口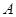 和一個運算出口
和一個運算出口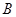 ,執行某種運算程序.
,執行某種運算程序.
(1)當從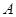 口輸入自然數
口輸入自然數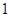 時,從
時,從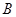 口得到實數
口得到實數 ,記為
,記為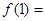
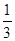 ;
;
(2)當從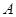 口輸入自然數
口輸入自然數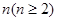 時,在
時,在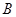 口得到的結果
口得到的結果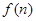 是前一結果
是前一結果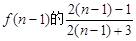 倍.
倍.
當從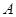 口輸入
口輸入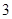 時,從
時,從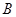 口得到 ;要想從
口得到 ;要想從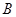 口得到
口得到 ,則應從
,則應從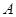 口輸入自然數 .
口輸入自然數 .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列{an}是等差數列,數列{bn}是等比數列,且對任意的n∈N*,都有a1b1+a2b2+a3b3+···+anbn=n·2n+3.
(1)若{bn}的首項為4,公比為2,求數列{an+bn}的前n項和Sn;
(2)若a1=8.
①求數列{an}與{bn}的通項公式;
②試探究:數列{bn}中是否存在某一項,它可以表示為該數列中其它r(r∈N,r≥2)項的和?若存在,請求出該項;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
數列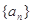 的前n項和記為
的前n項和記為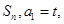 點
點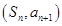 在直線
在直線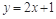 上,
上,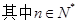 .(1)若數列
.(1)若數列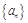 是等比數列,求實數
是等比數列,求實數 的值;
的值;
(2)設各項均不為0的數列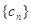 中,所有滿足
中,所有滿足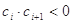 的整數
的整數 的個數稱為這個數列
的個數稱為這個數列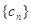 的“積異號數”,令
的“積異號數”,令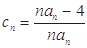 (
(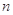
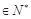 ),在(1)的條件下,求數列
),在(1)的條件下,求數列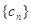 的“積異號數”
的“積異號數”
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知集合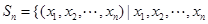 是正整數
是正整數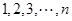 的一個排列
的一個排列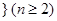 ,函數
,函數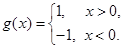 對于
對于 ,定義:
,定義: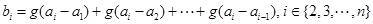 ,
,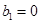 ,稱
,稱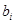 為
為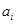 的滿意指數.排列
的滿意指數.排列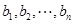 為排列
為排列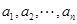 的生成列;排列
的生成列;排列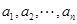 為排列
為排列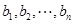 的母列.
的母列.
(Ⅰ)當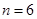 時,寫出排列
時,寫出排列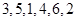 的生成列及排列
的生成列及排列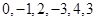 的母列;
的母列;
(Ⅱ)證明:若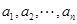 和
和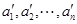 為
為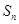 中兩個不同排列,則它們的生成列也不同;
中兩個不同排列,則它們的生成列也不同;
(Ⅲ)對于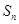 中的排列
中的排列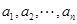 ,定義變換
,定義變換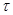 :將排列
:將排列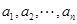 從左至右第一個滿意指數為負數的項調至首項,其它各項順序不變,得到一個新的排列.證明:一定可以經過有限次變換
從左至右第一個滿意指數為負數的項調至首項,其它各項順序不變,得到一個新的排列.證明:一定可以經過有限次變換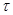 將排列
將排列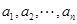 變換為各項滿意指數均為非負數的排列.
變換為各項滿意指數均為非負數的排列.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
項數為n的數列a1,a2,a3,…,an的前k項和為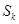 (k=1,2,3,…,n),定義
(k=1,2,3,…,n),定義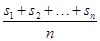 為該項數列的“凱森和”,如果項系數為99項的數列a1,a2,a3,…,a99的“凱森和”為1 000,那么項數為100的數列100,a1,a2,a3,…,a99的“凱森和”為( )
為該項數列的“凱森和”,如果項系數為99項的數列a1,a2,a3,…,a99的“凱森和”為1 000,那么項數為100的數列100,a1,a2,a3,…,a99的“凱森和”為( )
| A.991 | B.1 001 | C.1 090 | D.1 100 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com