
【題目】已知 ![]() 的內切圓
的內切圓![]() 切邊
切邊![]() 于點
于點![]() , 而
, 而![]() 是邊
是邊![]() 上的任意內點.設
上的任意內點.設![]() 和
和![]() 的內切圓圓心分別是
的內切圓圓心分別是![]() 和
和![]() .
.
(1)求證:∠I1DI2 =90°(即![]() 、
、![]() 、
、![]() 、
、![]() 四點共圓);
四點共圓);
(2)設![]() 、
、![]() 、
、![]() 、
、![]() 四點所在的圓周的半徑為
四點所在的圓周的半徑為![]() , 而
, 而![]() 的內切圓半徑為
的內切圓半徑為![]() ,試求
,試求![]() 的取值范圍(
的取值范圍(![]() 取遍各種形狀的三角形,點
取遍各種形狀的三角形,點![]() 取遍邊
取遍邊![]() 上的每一個內點).
上的每一個內點).
【答案】(1)見解析;(2)![]()
【解析】
(1)如圖,聯結 ![]() 、
、![]() 、
、![]() .由
.由![]() 平分
平分![]() 及
及![]() 平 分
平 分![]() ,易 知
,易 知![]() =90 °.
=90 °.
故只須證明![]() 、
、![]() 、
、![]() 、
、![]() 四點共圓, 而這只須證明
四點共圓, 而這只須證明![]() .
.
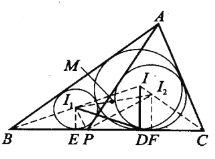
設![]() 切
切![]() 于點
于點![]() ,則
,則![]() .只須證明
.只須證明![]() ,
,
亦只須證明![]() ,即
,即![]() . ①
. ①
設![]() 切
切![]() 于點
于點![]() ,聯結
,聯結![]() ,則
,則![]() .
.
由于![]() ,故
,故![]() .
.
從而,![]() .
.
所以, ![]() .
.
于是,![]() ,即
,即![]() . ②
. ②
由式①、②可知, 只須證明![]() . ③
. ③
欲證式③, 只須證明![]() . ④
. ④
由切線長相等得![]() ,
,
即式④、③確實成立.
再由式 ②可推出式 ①成立, 從而,![]() ,即
,即![]() 、
、![]() 、
、![]() 、
、![]() 四點共圓.
四點共圓.
因此,![]() .
.
(2)由(1)知![]() 、
、![]() 、
、![]() 、
、![]() 四點共圓,
四點共圓,![]() ,所以,
,所以,![]() .
.
顯然,![]() 、
、![]() 、
、![]() 三點共線,
三點共線,![]() 、
、![]() 、
、![]() 也三點共線,且
也三點共線,且
![]() .
.
取![]() 的中點
的中點![]() ,則
,則![]() 是
是![]() 、
、![]() 、
、![]() 、
、![]() 四點所在圓周的圓心,
四點所在圓周的圓心,![]() 為該圓直徑.由于
為該圓直徑.由于![]() ,所以,點
,所以,點![]() 必在⊙
必在⊙![]() 的內部.從而,
的內部.從而,![]() 必不是直徑.
必不是直徑.
于是,![]() ,即
,即![]() .故
.故![]() .
.
若固定![]() 不變,且
不變,且![]() ,當
,當![]() ,且
,且![]() 為
為![]() 的中點,則
的中點,則![]() ,即
,即![]() .
.
若固定![]() 不變,當
不變,當![]() 且
且![]() 為
為![]() 上的定點,
上的定點,![]() ,
,
![]() (定值),這時,
(定值),這時,![]() .
.
再由幾何圖形變化的連續性可知,![]() 可取遍開區間
可取遍開區間![]() 內的所有值.
內的所有值.
綜上可知, ![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】12個朋友每周聚餐一次,每周他們分成三組,每組4人,不同組坐不同的桌子.若要求這些朋友中任意兩個人至少有一次同坐一張桌子,則至少需要周____周.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是正整數,且
是正整數,且![]() .(1)試求出最大的正整數
.(1)試求出最大的正整數![]() ,使得存在各邊長都是不大于
,使得存在各邊長都是不大于![]() 的正整數,且任意兩邊之差(大減小)都不小于k的三角形;(2)試求出所有的正整數
的正整數,且任意兩邊之差(大減小)都不小于k的三角形;(2)試求出所有的正整數![]() ,使得(1)中所述的對應于最大的正整數
,使得(1)中所述的對應于最大的正整數![]() 的三角形有且只有一個.
的三角形有且只有一個.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 定義域為
定義域為![]() ,部分對應值如表,
,部分對應值如表,![]() 的導函數
的導函數![]() 的圖象如圖所示. 下列關于函數
的圖象如圖所示. 下列關于函數![]() 的結論正確的有( )
的結論正確的有( )
|
|
|
|
|
|
|
|
|
|
|
|

A.函數![]() 的極大值點有
的極大值點有![]() 個
個
B.函數在![]() 上
上![]() 是減函數
是減函數
C.若![]() 時,
時,![]() 的最大值是
的最大值是![]() ,則
,則![]() 的最大值為4
的最大值為4
D.當![]() 時,函數
時,函數![]() 有
有![]() 個零點
個零點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解某省各景點在大眾中的熟知度,隨機對15~65歲的人群抽樣了![]() 人,回答問題“某省有哪幾個著名的旅游景點?”統計結果如下圖表
人,回答問題“某省有哪幾個著名的旅游景點?”統計結果如下圖表
組號 | 分組 | 回答正確 的人數 | 回答正確的人數 占本組的頻率 |
第1組 | [15,25) |
| 0.5 |
第2組 | [25,35) | 18 |
|
第3組 | [35,45) |
| 0.9 |
第4組 | [45,55) | 9 | 0.36 |
第5組 | [55,65] | 3 |
|

(1)分別求出![]() 的值;
的值;
(2)從第2,3,4組回答正確的人中用分層抽樣的方法抽取6人,求第2,3,4組每組各抽取多少人?
(3)在(2)抽取的6人中隨機抽取2人,求所抽取的人中恰好沒有第3組人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個不透明的袋子中裝有4個完全相同的小球,球上分別標有數字為0,1,2,3.現甲從中摸出1個球后放回,乙再從中摸出1個球,誰摸出的球上的數字大誰獲勝,則甲、乙各摸一次球后,甲獲勝且乙摸出的球上數字為偶數的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,若橢圓經過點
,若橢圓經過點![]() ,且
,且![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設斜率為![]() 的直線
的直線![]() 與以原點為圓心,半徑為
與以原點為圓心,半徑為![]() 的圓交于
的圓交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,當
,當![]() 取得最小值時,求直線
取得最小值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com