
【題目】某文化創意公司開發出一種玩具(單位:套)進行生產和銷售.根據以往經驗,每月生產x套玩具的成本p由兩部分費用(單位:元)構成:![]() .固定成本(與生產玩具套數x無關),總計一百萬元;b.生產所需的直接總成本
.固定成本(與生產玩具套數x無關),總計一百萬元;b.生產所需的直接總成本![]() .
.
(1)問:該公司每月生產玩具多少套時,可使得平均每套所需成本費用最少?此時每套玩具的成本費用是多少?
(2)假設每月生產出的玩具能全部售出,但隨著x的增大,生產所需的直接總成本在急劇增加,因此售價也需隨著x的增大而適當增加.設每套玩具的售價為q元,![]() (
(![]() ).若當產量為15000套時利潤最大,此時每套售價為300元,試求
).若當產量為15000套時利潤最大,此時每套售價為300元,試求![]() 、b的值.(利潤=銷售收入-成本費用)
、b的值.(利潤=銷售收入-成本費用)
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某“雙一流”大學專業獎學金是以所學專業各科考試成績作為評選依據,分為專業一等獎學金(獎金額![]() 元)、專業二等獎學金(獎金額
元)、專業二等獎學金(獎金額![]() 元)及專業三等獎學金(獎金額
元)及專業三等獎學金(獎金額![]() 元),且專業獎學金每個學生一年最多只能獲得一次.圖(1)是統計了該校
元),且專業獎學金每個學生一年最多只能獲得一次.圖(1)是統計了該校![]() 年
年![]() 名學生周課外平均學習時間頻率分布直方圖,圖(2)是這
名學生周課外平均學習時間頻率分布直方圖,圖(2)是這![]() 名學生在
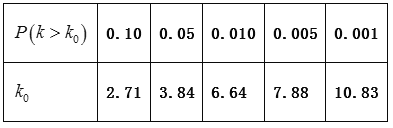
名學生在![]() 年周課外平均學習時間段獲得專業獎學金的頻率柱狀圖.
年周課外平均學習時間段獲得專業獎學金的頻率柱狀圖.
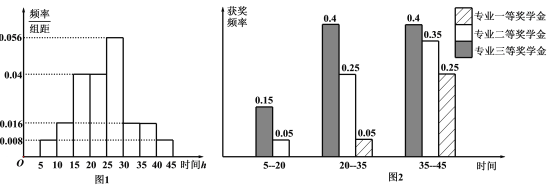
(Ⅰ)求這![]() 名學生中獲得專業三等獎學金的人數;
名學生中獲得專業三等獎學金的人數;
(Ⅱ)若周課外平均學習時間超過![]() 小時稱為“努力型”學生,否則稱為“非努力型”學生,列
小時稱為“努力型”學生,否則稱為“非努力型”學生,列![]() 聯表并判斷是否有
聯表并判斷是否有![]() 的把握認為該校學生獲得專業一、二等獎學金與是否是“努力型”學生有關?
的把握認為該校學生獲得專業一、二等獎學金與是否是“努力型”學生有關?
(Ⅲ)若以頻率作為概率,從該校任選一名學生,記該學生![]() 年獲得的專業獎學金額為隨機變量
年獲得的專業獎學金額為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中點.
,E是SA的中點.
(1)求證:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED與平面SBC所成二面角(銳角)的大小.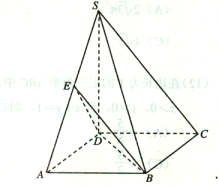
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABCA1B1C1中,D,E,F分別是B1C1,AB,AA1的中點.
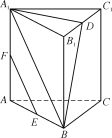
(1) 求證:EF∥平面A1BD;
(2) 若A1B1=A1C1,求證:平面A1BD⊥平面BB1C1C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,中美貿易摩擦不斷.特別是美國對我國華為的限制.盡管美國對華為極力封鎖,百般刁難,并不斷加大對各國的施壓,拉攏他們抵制華為5G,然而這并沒有讓華為卻步.華為在2018年不僅凈利潤創下記錄,海外增長同樣強勁.今年,我國華為某一企業為了進一步增加市場競爭力,計劃在2020年利用新技術生產某款新手機.通過市場分析,生產此款手機全年需投入固定成本250萬,每生產![]() (千部)手機,需另投入成本
(千部)手機,需另投入成本![]() 萬元,且
萬元,且  ,由市場調研知,每部手機售價0.7萬元,且全年內生產的手機當年能全部銷售完.
,由市場調研知,每部手機售價0.7萬元,且全年內生產的手機當年能全部銷售完.
(![]() )求出2020年的利潤
)求出2020年的利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千部)的函數關系式,(利潤=銷售額—成本);
(千部)的函數關系式,(利潤=銷售額—成本);
![]() 2020年產量為多少(千部)時,企業所獲利潤最大?最大利潤是多少?
2020年產量為多少(千部)時,企業所獲利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 中點,
中點,![]() .
.
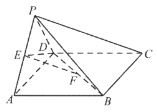
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 平面
平面![]() ?若存在,指出點
?若存在,指出點![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海輪每小時使用的燃料費與它的航行速度的立方成正比,已知某海輪的最大航速為![]() 海里/小時, 當速度為
海里/小時, 當速度為![]() 海里/小時時,它的燃料費是每小時
海里/小時時,它的燃料費是每小時![]() 元,其余費用(無論速度如何)都是每小時
元,其余費用(無論速度如何)都是每小時![]() 元.如果甲乙兩地相距
元.如果甲乙兩地相距![]() 海里,則要使該海輪從甲地航行到乙地的總費用最低,它的航速應為( )
海里,則要使該海輪從甲地航行到乙地的總費用最低,它的航速應為( )
A.![]() 海里/小時B.
海里/小時B.![]() 海里/小時
海里/小時
C.![]() 海里/小時D.
海里/小時D.![]() 海里/小時
海里/小時
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:極坐標與參數方程
已知在一個極坐標系中點![]() 的極坐標為
的極坐標為![]() .
.
(1)求出以![]() 為圓心,半徑長為2的圓的極坐標方程(寫出解題過程)并畫出圖形.
為圓心,半徑長為2的圓的極坐標方程(寫出解題過程)并畫出圖形.
(2)在直角坐標系中,以圓![]() 所在極坐標系的極點為原點,極軸為
所在極坐標系的極點為原點,極軸為![]() 軸的正半軸建立直角坐標系,點
軸的正半軸建立直角坐標系,點![]() 是圓
是圓![]() 上任意一點,
上任意一點, ![]() ,
, ![]() 是線段
是線段![]() 的中點,當點
的中點,當點![]() 在圓
在圓![]() 上運動時,求點
上運動時,求點![]() 的軌跡的普通方程.
的軌跡的普通方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com