
���}Ŀ����֪�E�A![]() ��
��![]() ��������c(di��n)�քe��C��D�����^(gu��)�c(di��n)
��������c(di��n)�քe��C��D�����^(gu��)�c(di��n)![]() ��P�ǙE�A�Ϯ���C��D������һ�c(di��n)��ֱ��PC��PD��б��֮�e��
��P�ǙE�A�Ϯ���C��D������һ�c(di��n)��ֱ��PC��PD��б��֮�e��![]() ��
��
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2��O������(bi��o)ԭ�c(di��n)���O(sh��)ֱ��CP����ֱ��x = m���c(di��n)M����(d��ng)m���ֵ�r(sh��)��![]() �鶨ֵ��
�鶨ֵ��
���𰸡���1��![]() ��2��
��2��![]()
��������
(1)�O(sh��)![]() ,����(j��)�}������
,����(j��)�}������![]() ,�ٴ�
,�ٴ�![]() ��E�A���̼������.
��E�A���̼������.
(2)����(j��)(1)�еĽY(ji��)Փ, �O(sh��)ֱ��![]() ,��(li��n)���c�E�A�ķ���,���
,��(li��n)���c�E�A�ķ���,���![]() ,
,![]() ,�ٱ��_(d��)��
,�ٱ��_(d��)��![]() ,����(j��)�������(w��n)�}���ϵ��(sh��)���P(gu��n)ϵ����.Ҳ��ֱ���O(sh��)
,����(j��)�������(w��n)�}���ϵ��(sh��)���P(gu��n)ϵ����.Ҳ��ֱ���O(sh��)![]() ���_(d��)��
���_(d��)��![]() ,����
,����![]() �M��E�A�ķ����M(j��n)�л���(ji��n),ͬ���ɵ�m��ֵ.
�M��E�A�ķ����M(j��n)�л���(ji��n),ͬ���ɵ�m��ֵ.
�⣺��1���E�A![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() ,��
,��![]() ,��
,��
����?y��n)�ֱ��![]() ��б��֮�e��
��б��֮�e��![]() ,��
,��![]() .
.
��![]() .��
.��![]() ,��
,��
(li��n)���٢ڵ�![]() ��
��
������ęE�A���̞�![]() ��
��
��2������1���ɣ�1��֪,![]() �����}����O(sh��)
�����}����O(sh��)![]() ,
,
��x=m,��![]() �����O(sh��)
�����O(sh��)![]()
�� �����ã�
�����ã�![]() ��
��
��![]() ,��
,��![]() ,
,![]() ,
,
����![]() ,
,
�� ,
,
Ҫʹ![]() �ck�o(w��)�P(gu��n),ֻ��
�ck�o(w��)�P(gu��n),ֻ��![]() ,�˕r(sh��)
,�˕r(sh��)![]() �����4.
�����4.
��![]()
����2��:�O(sh��)![]() ,�t
,�t![]() ,��x=m,��
,��x=m,��![]() ,
,
��![]()
��![]() ��
��![]() ,
,
����![]() ,
,
Ҫʹ![]() �c
�c![]() �o(w��)�P(gu��n),ֻ�
�o(w��)�P(gu��n),ֻ�![]() ,�˕r(sh��)
,�˕r(sh��)![]() .
.
��![]()



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��������![]() ���c(di��n)
���c(di��n)![]() ̎���о����̞�
̎���о����̞�![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() ��(d��o)����(sh��)
�Č�(d��o)����(sh��)![]() ���ڃɂ�(g��)����ȵ����c(di��n)����(sh��)��(sh��)
���ڃɂ�(g��)����ȵ����c(di��n)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��3����(d��ng)![]() �r(sh��)���Ƿ��������(sh��)
�r(sh��)���Ƿ��������(sh��)![]() ��ʹ���P(gu��n)��
��ʹ���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ������������ڣ����
������������ڣ����![]() �����ֵ���������ڣ��f(shu��)������.
�����ֵ���������ڣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() (
(![]() )�����ҽ��c(di��n)�քe��
)�����ҽ��c(di��n)�քe��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ������c(di��n)���c(di��n)
������c(di��n)���c(di��n)![]() ��
��![]() �ϣ�
�ϣ�![]() ����
����![]() .
.
��1����![]() �ķ��̣�
�ķ��̣�
��2����֪�^(gu��)ԭ�c(di��n)��ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)����ֱ��
���c(di��n)����ֱ��![]() ��ֱ��
��ֱ��![]() �^(gu��)
�^(gu��)![]() ���c�E�A
���c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f(x)��4x��3sinx��x��(��1��1)�����f(1��a)��f(1��a2)<0�������t��(sh��)��(sh��)a��ȡֵ������(����)
A. (0,1) B. ![]() C.
C. ![]() D. (���ޣ���2)��(1������)
D. (���ޣ���2)��(1������)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����˽��\(y��n)��(d��ng)����p�ʵ�Ч����ij�������{(di��o)����20�������ߣ�����֮ǰ�������w����r�����SD��1����ʾ����(j��ng)�^(gu��)�Ă�(g��)�µĽ������������w����r�����SD��2����ʾ����(du��)�Ƚ���ǰ���P(gu��n)���@20�������ߣ�����Y(ji��)Փ�����_���ǣ� ��
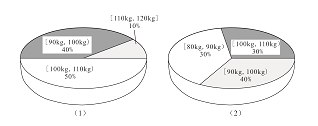
A.�����������w���څ^(q��)�g[90kg��100kg����(n��i)���˔�(sh��)��׃
B.�����������w���څ^(q��)�g[100kg��110kg����(n��i)���˔�(sh��)�p����4��
C.�����������@20λ�������w�ص���λ��(sh��)λ��[90kg��100kg��
D.����������ԭ��(l��i)�w����[110kg��120kg]��(n��i)�ķ������w�ض����ٜp�p��10kg
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���S�ӹ�ij�N�����Ҫ��(j��ng)�^(gu��)![]() ��
��![]() ��
��![]() ����������ÿ������ļӹ������(d��)������������ӹ��ϸ�ĸ��ʷքe��
����������ÿ������ļӹ������(d��)������������ӹ��ϸ�ĸ��ʷքe��![]() ��
��![]() ��
��![]() .�������ϸ�������һ��(j��)Ʒ��ǡ�Ѓɵ�����ϸ����������(j��)Ʒ����������UƷ���Ҽӹ�һ��(g��)��������(j��)Ʒ�ĸ��ʞ�
.�������ϸ�������һ��(j��)Ʒ��ǡ�Ѓɵ�����ϸ����������(j��)Ʒ����������UƷ���Ҽӹ�һ��(g��)��������(j��)Ʒ�ĸ��ʞ�![]() .
.
��1����![]() ��
��
��2����ԓ�����һ��(j��)Ʒÿ��(g��)�ɫ@��200Ԫ������(j��)Ʒÿ��(g��)�ɫ@��100Ԫ��ÿ��(g��)�UƷ��ʹ���S�pʧ50Ԫ���O(sh��)һ��(g��)�����(j��ng)�^(gu��)��������ӹ�����K�@����![]() Ԫ����
Ԫ����![]() �ķֲ��м���(sh��)�W(xu��)����.
�ķֲ��м���(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]() ��������(sh��)
��������(sh��)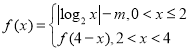 ��4��(g��)��ͬ�����c(di��n)
��4��(g��)��ͬ�����c(di��n)![]() ����
����![]() ���t
���t![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�ɶ��c(di��n)![]() ��
��![]() ���c(di��n)P�M��
���c(di��n)P�M��![]() .
.
��1�����c(di��n)P��܉�EC�ķ��̣�
��2����![]() ��ֱ��l�c܉�EC����A��B���c(di��n)��
��ֱ��l�c܉�EC����A��B���c(di��n)��![]() ��
��![]() ��б��֮�͞�2����(w��n)ֱ��l�Ƿ���^(gu��)���c(di��n)�����^(gu��)���c(di��n)��������c(di��n)������(bi��o)�������^(gu��)���c(di��n)��Ո(q��ng)�f(shu��)������.
��б��֮�͞�2����(w��n)ֱ��l�Ƿ���^(gu��)���c(di��n)�����^(gu��)���c(di��n)��������c(di��n)������(bi��o)�������^(gu��)���c(di��n)��Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
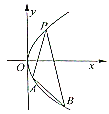
���}Ŀ����D���^(gu��)���タ![]() ��һ�c(di��n)
��һ�c(di��n)![]() �����ɗlֱ���քe�����タ��
�����ɗlֱ���քe�����タ��![]() ��
��![]() ����(d��ng)
����(d��ng)![]() �c
�c![]() ��б�ʴ����҃Aб�ǻ��a(b��)�r(sh��)��
��б�ʴ����҃Aб�ǻ��a(b��)�r(sh��)��
��������![]() ��ֵ��
��ֵ��
��������ֱ��![]() ��
��![]() �S�ϵĽؾ�
�S�ϵĽؾ�![]() �r(sh��)����
�r(sh��)����![]() ��e
��e![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com