
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() 和
和![]() ,過點
,過點![]() 的直線與橢圓交于
的直線與橢圓交于![]() 軸上方的
軸上方的![]() ,
,![]() 兩點,且
兩點,且![]() .
.
(Ⅰ)求橢圓的離心率;
(Ⅱ)(ⅰ)求直線![]() 的斜率;
的斜率;
(ⅱ)設點![]() 與點
與點![]() 關于坐標原點對稱,直線
關于坐標原點對稱,直線![]() 上有一點
上有一點![]() 在
在![]() 的外接圓上,求
的外接圓上,求![]() 的值.
的值.
【答案】(1) 離心率![]() ;(2)
;(2) ![]() ,
,![]() .
.
【解析】分析:(1)由![]() 得
得![]() ,化為
,化為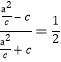 ,從而可得結果;(2) (i)由(1)可設圓的方程可寫
,從而可得結果;(2) (i)由(1)可設圓的方程可寫![]() ,設直線AB的方程為
,設直線AB的方程為![]() ,聯立,結合點B為線段AE的中點可得
,聯立,結合點B為線段AE的中點可得![]() ,
,![]() ,從而可得結果;(ii)由(i)可知
,從而可得結果;(ii)由(i)可知![]()
當![]() 時,得
時,得![]() ,由已知得
,由已知得![]() ,求出外接圓方程與直線
,求出外接圓方程與直線![]() 的方程,聯立可得結果.
的方程,聯立可得結果.
詳解:(1)由![]() 得
得![]() ,
,
從而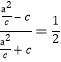
整理,得![]() ,
,
故離心率![]()
(2) 解法一:(i)由(I)得![]() ,所以橢圓的方程可寫
,所以橢圓的方程可寫![]()
設直線AB的方程為![]() ,即
,即![]() .
.
由已知設![]() ,則它們的坐標滿足方程組
,則它們的坐標滿足方程組![]()
消去y整理,得![]() .
.
依題意,![]()
而 ![]() ①
①
![]() ②w
②w
由題設知,點B為線段AE的中點,所以
![]() ③
③
聯立①③解得 ![]() ,
,![]()
將![]() 代入②中,解得
代入②中,解得![]() .
.
解法二:![]() 利用中點坐標公式求出
利用中點坐標公式求出![]() ,帶入橢圓方程
,帶入橢圓方程
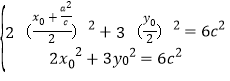 消去
消去![]() ,解得
,解得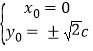 解出
解出![]()
(依照解法一酌情給分)
(ii)由(i)可知![]()
當![]() 時,得
時,得![]() ,由已知得
,由已知得![]() .
.
線段![]() 的垂直平分線l的方程為
的垂直平分線l的方程為![]()
直線l與x軸的交點![]() 是
是![]() 外接圓的圓心,因此外接圓的方程為
外接圓的圓心,因此外接圓的方程為![]() .
.
直線![]() 的方程為
的方程為
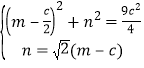 ,
,
由![]() 解得
解得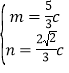 故
故![]()


科目:高中數學 來源: 題型:
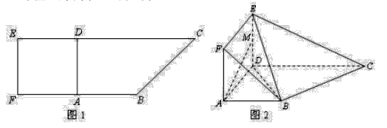
【題目】如圖 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .現以
.現以![]() 為一邊向外作正方形
為一邊向外作正方形![]() ,然后沿邊
,然后沿邊![]() 將正方形
將正方形![]() 翻折,使
翻折,使![]() 平面與平面
平面與平面![]() 垂直,
垂直, ![]() 為
為![]() 的中點,如圖 2.
的中點,如圖 2.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證: ![]() 平面
平面![]() ;
;
(3)求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的方程為
的方程為![]() .以坐標原點為極點,
.以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 有且僅有三個公共點,求
有且僅有三個公共點,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
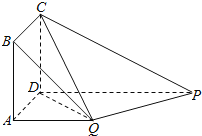
【題目】如圖,四邊形ABCD為正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
(1)證明:平面PQC⊥平面DCQ;
(2)求直線DQ與面PQC成角的正弦值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近來國內一些互聯網公司為了贏得更大的利潤、提升員工的奮斗姿態,要求員工實行![]() 工作制,即工作日早
工作制,即工作日早![]() 點上班,晚上
點上班,晚上![]() 點下班,中午和傍晚最多休息
點下班,中午和傍晚最多休息![]() 小時,總計工作
小時,總計工作![]() 小時以上,并且一周工作
小時以上,并且一周工作![]() 天的工作制度,工作期間還不能請假,也沒有任何補貼和加班費.消息一出,社交媒體一片嘩然,有的人認為這是違反《勞動法》的一種對員工的壓榨行為,有的人認為只有付出超越別人的努力和時間,才能夠實現想要的成功,這是提升員工價值的一種有效方式.對此,國內某大型企業集團管理者認為應當在公司內部實行
天的工作制度,工作期間還不能請假,也沒有任何補貼和加班費.消息一出,社交媒體一片嘩然,有的人認為這是違反《勞動法》的一種對員工的壓榨行為,有的人認為只有付出超越別人的努力和時間,才能夠實現想要的成功,這是提升員工價值的一種有效方式.對此,國內某大型企業集團管理者認為應當在公司內部實行![]() 工作制,但應該給予一定的加班補貼(單位:百元),對于每月的補貼數額集團人力資源管理部門隨機抽取了集團內部的
工作制,但應該給予一定的加班補貼(單位:百元),對于每月的補貼數額集團人力資源管理部門隨機抽取了集團內部的![]() 名員工進行了補貼數額(單位:百元)期望值的網上問卷調查,并把所得數據列成如下所示的頻數分布表:
名員工進行了補貼數額(單位:百元)期望值的網上問卷調查,并把所得數據列成如下所示的頻數分布表:
組別(單位:百元) |
|
|
|
|
|
頻數(人數) |
|
|
|
|
|
(Ⅰ)求所得樣本的中位數(精確到百元);
(Ⅱ)根據樣本數據,可近似地認為員工的加班補貼X服從正態分布![]() ,若該集團共有員工
,若該集團共有員工![]() ,試估計有多少員工期待加班補貼在
,試估計有多少員工期待加班補貼在![]() 元以上;
元以上;
(Ⅲ)已知樣本數據中期望補貼數額在![]() 范圍內的
范圍內的![]() 名員工中有
名員工中有![]() 名男性,
名男性,![]() 名女性,現選其中
名女性,現選其中![]() 名員工進行消費調查,記選出的女職員人數為
名員工進行消費調查,記選出的女職員人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分,(1)小問7分,(2)小問5分)
設函數![]()
(1)若![]() 在
在![]() 處取得極值,確定
處取得極值,確定![]() 的值,并求此時曲線
的值,并求此時曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() 在
在![]() 上為減函數,求
上為減函數,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確的命題的是( )
A.已知隨機變量服從二項分布![]() ,若
,若![]() ,
,![]() ,則
,則![]() ;
;
B.將一組數據中的每個數據都加上同一個常數后,方差恒不變;
C.設隨機變量![]() 服從正態分布
服從正態分布![]() ,若
,若![]() ,則
,則![]() ;
;
D.某人在10次射擊中,擊中目標的次數為![]() ,
,![]() ,則當
,則當![]() 時概率最大.
時概率最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com