
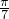 +sin
+sin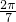 +…+sin
+…+sin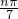 (n∈N+),則在S1,S2,…S100中,正數的個數是________.
(n∈N+),則在S1,S2,…S100中,正數的個數是________.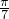 >0,sin
>0,sin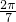 >0,…,sin
>0,…,sin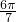 >0,sin
>0,sin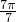 =0,sin
=0,sin <0,…,sin
<0,…,sin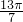 <0,sin
<0,sin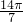 =0,
=0,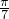 >0,
>0,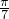 +sin
+sin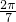 >0,…,
>0,…,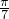 +sin
+sin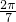 +…+sin
+…+sin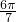 +sin
+sin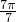 +sin
+sin =sin
=sin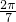 +…+sin
+…+sin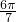 +sin
+sin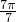 >0,
>0,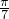 +sin
+sin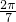 +…+sin
+…+sin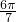 +sin
+sin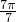 +sin
+sin +sin
+sin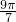 +…+sin
+…+sin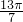 =0,
=0,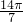 =0+0=0,
=0+0=0,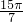 =0+sin
=0+sin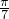 =S1>0,S16=S2>0,…S27=S13=0,S28=S14=0,
=S1>0,S16=S2>0,…S27=S13=0,S28=S14=0,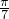 >0,sin
>0,sin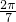 >0,…,sin
>0,…,sin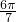 >0,sin
>0,sin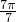 =0,sin
=0,sin <0,…,sin
<0,…,sin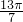 <0,sin
<0,sin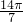 =0,可得到S1>0,…S13>0,而S14=0,從而可得到周期性的規律,從而得到答案.
=0,可得到S1>0,…S13>0,而S14=0,從而可得到周期性的規律,從而得到答案.

 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
| π |
| 7 |
| 2π |
| 7 |
| nπ |
| 7 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省莆田八中高二(上)期中數學試卷(文科)(解析版) 題型:解答題
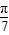 +sin
+sin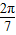 +…+sin
+…+sin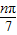 (n∈N+),則在S1,S2,…S100中,正數的個數是______.
(n∈N+),則在S1,S2,…S100中,正數的個數是______.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com